Refine listing
Actions for selected content:
1446 results in 60Kxx
Product forms based on backward traffic equations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 508-518
- Print publication:
- June 1995
-
- Article
- Export citation
On the saturation rule for the stability of queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 494-507
- Print publication:
- June 1995
-
- Article
- Export citation
Pathological behaviour in loss networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 519-533
- Print publication:
- June 1995
-
- Article
- Export citation
A limit theorem for the replication time of a DNA molecule
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 296-303
- Print publication:
- June 1995
-
- Article
- Export citation
Characterizing the idle-period distribution of GI/G/1 queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 247-255
- Print publication:
- March 1995
-
- Article
- Export citation
An optimal inspection–repair–replacement policy for standby systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 212-223
- Print publication:
- March 1995
-
- Article
- Export citation
On the asymptotic size and duration of a class of epidemic models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 11-24
- Print publication:
- March 1995
-
- Article
- Export citation
The mean waiting time of a GI/G/1 queue in light traffic via random thinning
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 256-266
- Print publication:
- March 1995
-
- Article
- Export citation
Equality of critical densities in continuum percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 90-104
- Print publication:
- March 1995
-
- Article
- Export citation
Loss networks under diverse routing: the symmetric star network
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 255-272
- Print publication:
- March 1995
-
- Article
- Export citation
Response time distributions in tandem G-networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 224-246
- Print publication:
- March 1995
-
- Article
- Export citation
Tight bounds on the sensitivity of generalised semi-Markov processes with a single generally distributed lifetime
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 63-73
- Print publication:
- March 1995
-
- Article
- Export citation
Note on generalizations of Mecke's formula and extensions of H = λG
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 105-122
- Print publication:
- March 1995
-
- Article
- Export citation
Limit laws for a stochastic process and random recursion arising in probabilistic modelling
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 185-202
- Print publication:
- March 1995
-
- Article
- Export citation
On the structure of an insensitive generalized semi-Markov process with reallocation and point-process input
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 203-225
- Print publication:
- March 1995
-
- Article
- Export citation
Asymptotic analysis of single resource loss systems in heavy traffic, with applications to integrated networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 273-292
- Print publication:
- March 1995
-
- Article
- Export citation
Dependencies in Markovian networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 226-254
- Print publication:
- March 1995
-
- Article
- Export citation
Computing the invariant law of a fluid model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 885-896
- Print publication:
- December 1994
-
- Article
- Export citation
The departure process of the M/G/1 queueing model with server vacation and exhaustive service discipline
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1070-1082
- Print publication:
- December 1994
-
- Article
- Export citation
Renewal-type behavior of absorption times in Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 988-1005
- Print publication:
- December 1994
-
- Article
- Export citation
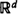 with density ρ, and add the origin as an extra point. Now connect any two points
with density ρ, and add the origin as an extra point. Now connect any two points 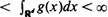 , then the two critical densities are non-trivial, i.e. bounded away from 0 and ∞. It is also known that if
, then the two critical densities are non-trivial, i.e. bounded away from 0 and ∞. It is also known that if 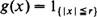 , for some
, for some 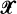 , and relates integrations concerning them to each other. For
, and relates integrations concerning them to each other. For 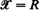 , we generalize this to a pair of random measures which are jointly stationary. The resulting formula extends the so-called Swiss Army formula, which was recently obtained as a generalization for Little's formula. The generalized Mecke formula, which is called GMF, can be also viewed as a generalization of the stationary version of
, we generalize this to a pair of random measures which are jointly stationary. The resulting formula extends the so-called Swiss Army formula, which was recently obtained as a generalization for Little's formula. The generalized Mecke formula, which is called GMF, can be also viewed as a generalization of the stationary version of 