Refine listing
Actions for selected content:
1446 results in 60Kxx
Optimal stochastic scheduling of forest networks with switching penalties
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 474-497
- Print publication:
- June 1994
-
- Article
- Export citation
Comparison of sequential and continuous inspection strategies for deteriorating systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 423-435
- Print publication:
- June 1994
-
- Article
- Export citation
An unreliable server characterization of the exponential distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 274-279
- Print publication:
- March 1994
-
- Article
- Export citation
The critical contact process on a homogeneous tree
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 250-255
- Print publication:
- March 1994
-
- Article
- Export citation
Burn-in and Maintenance Policies
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 207-221
- Print publication:
- March 1994
-
- Article
- Export citation
The Service Time Properties of an Unreliable Server Characterize the Exponential Distribution
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 172-182
- Print publication:
- March 1994
-
- Article
- Export citation
On simulation of random vectors by given densities in regions and on their boundaries
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 205-220
- Print publication:
- March 1994
-
- Article
- Export citation
On the MX/G/∞ queue by heterogeneous customers in a batch
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 280-286
- Print publication:
- March 1994
-
- Article
- Export citation
Conditioned Limit Theorems for the Difference of Waiting Time and Queue Length
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 242-257
- Print publication:
- March 1994
-
- Article
- Export citation
Shock models by underlying counting process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 156-166
- Print publication:
- March 1994
-
- Article
- Export citation
Replacement of train wheels: an application of dynamic reversal of a Markov process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-8
- Print publication:
- March 1994
-
- Article
- Export citation
A Central Limit Theorem for Cumulative Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 104-121
- Print publication:
- March 1994
-
- Article
- Export citation
Time-dependent rate conservation laws for a process defined with a stationary marked point process and their applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 114-129
- Print publication:
- March 1994
-
- Article
- Export citation
Sample Path Criteria for Weak Majorization
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 155-171
- Print publication:
- March 1994
-
- Article
- Export citation
AB percolation on plane triangulations is unimodal
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 193-204
- Print publication:
- March 1994
-
- Article
- Export citation
Simpler proofs of some properties of the fundamental period of the MAP/G/1 queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 235-243
- Print publication:
- March 1994
-
- Article
- Export citation
Distribution of the final extent of a rumour process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 244-249
- Print publication:
- March 1994
-
- Article
- Export citation
Networks of non-homogeneous M/G/∞ systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue A / 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 157-168
- Print publication:
- 1994
-
- Article
- Export citation
Transient analysis of M/M/1 queues in discrete time by general server vacations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue A / 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 115-129
- Print publication:
- 1994
-
- Article
- Export citation
On termination time processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue A / 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 325-336
- Print publication:
- 1994
-
- Article
- Export citation
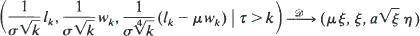 as
as 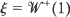 ,
, 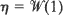 ,
, 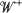 and
and 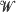 are independent,
are independent, 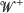 is a Brownian meander and
is a Brownian meander and 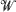 is a Wiener process. A similar result is also given for the difference of virtual waiting time and queue length processes. These results are also extended to a wider class of queueing systems than
is a Wiener process. A similar result is also given for the difference of virtual waiting time and queue length processes. These results are also extended to a wider class of queueing systems than 