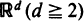A continuum percolation model on is considered. Using a renormalization technique developed by Grimmett and Marstrand, we show a continuum analogue of their results. We prove the critical value of the percolation equals the limit of the critical value of a slice as the thickness of the slice tends to infinity. We also prove that the effective conductivity in the model is bounded from below by a positive constant in the supercritical case.

Interacting particle systems provide an attractive framework for modelling the growth and spread of biological populations and diseases. One problem with their use in applications is that in most cases the existing information about their critical values and equilibrium densities is too crude to be useful. In this paper we describe a method for estimating these quantities that does not require very much computer time and produces fairly accurate results.

A simple model for the intensity of infection during an epidemic in a closed population is studied. It is shown that the size of an epidemic (i.e. the number of persons infected) and the cumulative force of an epidemic (i.e. the amount of infectiousness that has to be avoided by a person that will stay uninfected during the entire epidemic) satisfy an equation of balance. Under general conditions, small deviances from this balance are, in large populations, asymptotically mixed normally distributed. For some special epidemic models the size of an asymptotically large epidemic is asymptotically normally distributed.

Motivated by the need of studying a subset of components, ‘separate' from the other components, we introduce a new definition of ‘marginal distribution'. This is done by fixing the lives of the other components, but without the ‘knowledge' of the components of interest. Formally this is done by minimally repairing the components of no interest up to a predetermined time. Preservation properties of these ‘conditional marginal distributions', with respect to several stochastic orderings, are obtained. Also, inheritance of positive dependence properties, by the conditional marginal distributions, is shown. In addition, the preservations of dynamic multivariate aging properties, by the dynamic conditional marginal distributions, are obtained. The definitions and results are illustrated by a set of examples. Some applications for modelling ‘combinations' of sets of random lifetimes, and for bounding complex sets of random lifetimes, are described.

Faddy (1990) has conjectured that the variability of a pure birth process is increased, relative to the linear case, if the birth rates are convex and decreased if they are concave. We prove the conjecture by relating variability to the correlation structure of certain more informative versions of the process. A correlation inequality due to Harris (1977) is used to derive the necessary positive and negative correlation results.

In this note, the strong limiting behaviour of busy periods in GI/G/1 queues is studied under the condition that the traffic intensity equals unity.

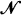A Markovian arrival stream is a marked point process generated by the state transitions of a given Markovian environmental process and Poisson arrival rates depending on the environment. It is shown that to a given marked point process there is a sequence of such Markovian arrival streams with the property that 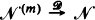as m →∞. Various related corollaries (involving stationarity, convergence of moments and ergodicity) and counterexamples are discussed as well.

Tandem queueing systems with blocking are frequently used in modelling of data communications and production transfer lines. We study such a system with no intermediate queues under the communication and the manufacturing blocking schemes and the assumption of just-in-time input. Explicit expressions for residence times, departure times, equilibrium throughput and some other measures of performance are obtained for the case of equal service requirements at all servers. This case is shown to be the ‘worst’ under the manufacturing blocking scheme, but not under the communication blocking scheme. An approximation formula is proposed for the equilibrium throughput in the case of exponential i.i.d. service times under the manufacturing blocking scheme.

A steady-state analysis of an M/G/1 queue with a finite capacity (K) and a finite population (N) of customers is given. The queue size distribution in this M/G/1/K/N system can be derived from the known queue size distribution in the corresponding M/G/1//N system. The system throughput, the mean response time, and the blocking probability are then calculated. The joint distributions of the queue size and the remaining service times are used to obtain the distributions of the unfinished work in the service facility and the waiting time of an accepted customer.

We obtain a single formula which, when its components are adequately chosen, transforms itself into the main formulas of the Palm theory of point processes: Little's L = λW formula [10], Brumelle's H = λG formula [5], Neveu's exchange formula [14], Palm inversion formula and Miyazawa's rate conservation law [12]. It also contains various extensions of the above formulas and some new ones.

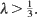In the biased annihilating branching process, particles place offspring on empty neighboring sites at rate A and destroy neighbors at rate 1. It is conjectured that for any λ ≥ 0 the population will spread to ∞, and this is shown in one dimension for The process on a finite graph when starting with a non-empty configuration has limiting distribution 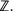v λ /(λ +1), the product measure with density λ/(1 +λ). 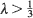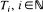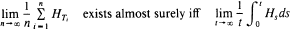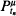It is shown that v λ /(λ +1) and δ Ø are the only stationary distributions on Moreover, if and the initial configuration is non-empty, then the limiting measure is v λ /(λ +1) provided the initial measure converges.

In this paper we introduce the concept of repair replacement. Repair replacement is a maintenance policy in which items are preventively maintained when a certain time has elapsed since their last repair. This differs from age replacement where a certain amount of time has elapsed since the last replacement. If the last repair was a complete repair, repair replacement is essentially the same as age replacement. It is in the case of minimal repair that these two policies differ. We make comparison between various types of policies in order to determine when and under which condition one type of policy is better than another.

It is known (Weizsäcker and Winkler (1990)) that for bounded predictable functions H and a Poisson process with jump times exists almost surely, and that in this case both limits are equal. Here we relax the boundedness condition on H. Our tool is a law of large numbers for local L 2-martingales. We show by examples that our condition is close to optimal. Furthermore we indicate a generalization to point processes on more general spaces. The above property is called PASTA (‘Poisson arrivals see time averages') and is heavily used in queueing theory.

The Type I and Type II counter models of Pyke (1958) have many applications in applied probability: in reliability, queueing and inventory models, for example. In this paper, we study the case in which the interarrival time distribution is of phase type. For the two counter models, we derive the renewal functions of the related renewal processes and propose approaches for their computations.

This paper is devoted to the study of a stationary G/G/1 queue in which work input is gradually injected into the system and the work load is processed at unit rate. First, assuming that the input process is stationary, the key formula for the stationary distribution of work in system is derived by appeal to the waiting time of the associated regular G/G/1 queue. The main contribution of this paper is the derivation of Laplace-Stieltjes transforms (LSTs) for the stationary distributions of work in system and related random variables in terms of integrations with respect to a waiting time distribution of the associated regular queue. The results are exemplified by giving explicit formulas for the LST of total work for M/Ek /1 and M/H 2/1. The results generalize the results of Pan et al. (1991) for the M/M/1 gradual input queue.

Using Palm-martingale calculus, we derive the workload characteristic function and queue length moment generating function for the BMAP/GI/1 queue with server vacations. In the queueing system under study, the server may start a vacation at the completion of a service or at the arrival of a customer finding an empty system. In the latter case we will talk of a server set-up time. The distribution of a set-up time or of a vacation period after a departure leaving a non-empty system behind is conditionally independent of the queue length and workload. Furthermore, the distribution of the server set-up times may be different from the distribution of vacations at service completion times. The results are particularized to the M/GI/1 queue and to the BMAP/GI/1 queue (without vacations).

We consider the problem of routing jobs to parallel queues with identical exponential servers and unequal finite buffer capacities. Service rates are state-dependent and non-decreasing with respect to queue lengths. We establish the extremal properties of the shortest non-full queue (SNQ) and the longest non-full queue (LNQ) policies, in systems with concave/convex service rates. Our analysis is based on the weak majorization of joint queue lengths which leads to stochastic orderings of critical performance indices. Moreover, we solve the buffer allocation problem, i.e. the problem of how to distribute a number of buffers among the queues. The two optimal allocation schemes are also ‘extreme', in the sense of capacity balancing. Some extensions are also discussed.

Given a parametric family of regenerative processes on a common probability space, we investigate when the derivatives (with respect to the parameter) are regenerative. We primarily consider sequences satisfying explicit, Lipschitz recursions, such as the waiting times in many queueing systems, and show that derivatives regenerate together with the original sequence under reasonable monotonicity or continuity assumptions. The inputs to our recursions are i.i.d. or, more generally, governed by a Harris-ergodic Markov chain. For i.i.d. input we identify explicit regeneration points; otherwise, we use coupling arguments. We give conditions for the expected steady-state derivative to be the derivative of the steady-state mean of the original sequence. Under these conditions, the derivative of the steady-state mean has a cycle-formula representation.

We show that for a large class of one-dimensional interacting particle systems, with a finite initial configuration, any limit measure , for a sequence of times tending to infinity, must be invariant. This result is used to show that the one-dimensional biased annihilating branching process with parameter > 1/3 converges in distribution to the upper invariant measure provided its initial configuration is almost surely finite and non-null.

In this paper we study the following general class of concurrent processing systems. There are several different classes of processors (servers) and many identical processors within each class. There is also a continuous random flow of jobs, arriving for processing at the system. Each job needs to engage concurrently several processors from various classes in order to be processed. After acquiring the needed processors the job begins to be executed. Processing is done non-preemptively, lasts for a random amount of time, and then all the processors are released simultaneously. Each job is specified by its arrival time, its processing time, and the list of processors that it needs to access simultaneously. The random flow (sequence) of jobs has a stationary and ergodic structure. There are several possible policies for scheduling the jobs on the processors for execution; it is up to the system designer to choose the scheduling policy to achieve certain objectives.

We focus on the effect that the choice of scheduling policy has on the asymptotic behavior of the system at large times and especially on its stability, under general stationary and ergocic input flows.