Lagrangian distributions are reviewed from the viewpoint of the Galton-Watson process. They are related to the busy period in queuing systems and to the first visit in random walks.

A property of the distributions is remarked for the application to vacant vehicles in a new transit system. Combinatorial identities of multinomial and binomial coefficients and related recurrences are shown by a probabilistic method. Based on the identities and recurrences, random forests generated by the Poisson and geometric Galton-Watson processes are characterized.

The class of new better than used in convex ordering (NBUC) is shown to be closed under formation of parallel systems with independent and identically distributed components.

Several queueing processes may be modeled as random walks on a multidimensional grid. In this paper the equilibrium distribution for the case of a two-dimensional grid is considered. In previous research it has been shown that for some two-dimensional random walks the equilibrium distribution has the form of an infinite series of products of powers which can be constructed with a compensation procedure. The object of the present paper is to investigate under which conditions such an elegant solution exists and may be found with a compensation approach. The conditions can be easily formulated in terms of the random behaviour in the inner area and the drift on the boundaries.

A carrier-borne epidemic is considered in which the carriers, subject to a death process, infect susceptibles by random allocation rather than the classical homogeneous mixing process. An explicit solution for the probability generating function (p.g.f.) of the process is obtained, and a probabilistic analysis of carrier models provided. The sizes and durations of the random allocation and classical carrier epidemics are compared. The strongest comparisons concern sample path results based on the probabilistic analysis; this also gives a sounder basis for computational work.

Particles may be removed from a lattice by murder, coalescence, mutual annihilation and simple death. If the particle system is not to die out, the removed particles must be replaced by births. This letter shows that coalescence can be counteracted by arbitrarily small birth-rates and contrasts this with the situations for annihilation and pure death where there are critical phenomena. The problem is unresolved for murder.

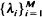This paper is concerned with the computation of asymptotic blocking probabilities for a generalized Erlangian system which results when M independent Poisson streams of traffic with rates access a trunk group of C circuits with traffic from stream k requiring Ak circuits which are simultaneously held and released after a time which is randomly distributed with unit mean and independent of earlier arrivals and holding times. A call from stream k is lost if on arrival less than Ak circuits are available. Although exact expressions for the blocking probabilities are known, their computation is unwieldy for even moderate-sized switches. It is shown that as the size of the switch increases in that both the traffic rates and trunk capacity are scaled together, simple asymptotic expressions for the blocking probabilities are obtained. In particular the expression is different for light, moderate and heavy loads. The approach is via exponential centering and large deviations and provides a unified framework for the analysis.

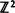We introduce and study a novel type of first-passage percolation problem on where the associated first-passage time measures the density of interface between two types of sites. If the types, designated + and –, are independently assigned their values with probability p and (1 — p) respectively, we show that the density of interface is non-zero provided that both species are subcritical with regard to percolation, i.e. pc > p > 1 – pc. Furthermore, we show that as p ↑ pc or p ↓ (1 – pc), the interface density vanishes with scaling behavior identical to the correlation length of the site percolation problem.

A number of papers have recently appeared in the literature in which customers, in moving from node to node in the network arrive as either a positive customer or as a batch of negative customers. A positive customer joining its queue increases the number of customers at the queue by 1 and each negative customer decreases the queue length by 1, if possible. It has been shown that the equilibrium distribution for these networks assumes a geometric product form, that certain partial balance equations prevail and that the parameters of the geometric distributions are, as in Jackson networks, the service facility throughputs of customers. In this paper the previous work is generalised by allowing state dependence into both the service and routing intensities and by allowing the possibility, although not the necessity, for negative customers to build up at the nodes.

A Markovian stochastic model for a system subject to random shocks is introduced. It is assumed that the shock arriving according to a Poisson process decreases the state of the system by a random amount. It is further assumed that the system is repaired by a repairman arriving according to another Poisson process if the state when he arrives is below a threshold α. Explicit expressions are deduced for the characteristic function of the distribution function of X(t), the state of the system at time t, and for the distribution function of X(t), if . 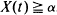The stationary case is also discussed.

Brownian flow systems, i.e. multidimensional Brownian motion with regulating barriers, can model queueing and inventory systems in which the behavior of different queues is correlated because of shared input processes. The behavior of such systems is typically difficult to describe exactly. We show how Brownian models of such systems, conditioned on one queue length exceeding a large value, decompose asymptotically into smaller subsystems. This conditioning induces a change in drift of the system's net input process and its components. The results here are analogous to results for jump-Markov queues recently obtained by Shwartz and Weiss. The Brownian setting leads to a simple description of the component processes' asymptotic behaviour, as well as to explicit distributional results.

In this paper, we consider period review (s, S) inventory systems with independent and identically distributed continuous demands and full backlogging. Using an approach recently proposed by Gong and Hu (1992), we derive an infinite system of linear equations for all moments of inventory level. Based on this infinite system, we develop two algorithms to calculate the moments of the inventory level. In the first one, we solve a finite system of linear equations whose solution converges to the moments as its dimension goes to infinity. In the second one, we in fact obtain the power series of the moments with respect to s and S. Both algorithms are based on some very simple recursive procedures. To show their efficiency and speed, we provide some numerical examples for the first algorithm.

(s, S) INVENTORY SYSTEMS; DYNAMIC RECURSIVE EQUATIONS; INFINITE LINEAR EQUATIONS; MACLAURIN SERIES

We derive expressions for the Laplace transform of the sojourn time density in a single-server queue with exponential service times and independent Poisson arrival streams of both ordinary, positive customers and negative customers which eliminate a positive customer if present. We compare first-come first-served and last-come first-served queueing disciplines for the positive customers, combined with elimination of the last customer in the queue or the customer in service by a negative customer. We also derive the corresponding result for processor-sharing discipline with random elimination. The results show differences not only in the Laplace transforms but also in the means of the distributions, in contrast to the case where there are no negative customers. The various combinations of queueing discipline and elimination strategy are ranked with respect to these mean values.

We analyze a class of stochastic and dynamic vehicle routing problems in which demands arrive randomly over time and the objective is minimizing waiting time. In our previous work ([6], [7]), we analyzed this problem for the case of uniformly distributed demand locations and Poisson arrivals. In this paper, using quite different techniques, we are able to extend our results to the more realistic case where demand locations have an arbitrary continuous distribution and arrivals follow only a general renewal process. Further, we improve significantly the best known lower bounds for this class of problems and construct policies that are provably within a small constant factor relative to the optimal solution. We show that the leading behavior of the optimal system time has a particularly simple form that offers important structural insight into the behavior of the system. Moreover, by distinguishing two classes of policies our analysis shows an interesting dependence of the system performance on the demand distribution.

The generalized queueing networks (G-networks) which we introduce in this paper contain customers and signals. Both customers and signals can be exogenous, or can be obtained by a Markovian movement of a customer from one queue to another after service transforming itself into a signal or remaining a customer. A signal entering a queue forces a customer to move instantaneously to another queue according to a Markovian routing rule, or to leave the network, while customers request service. This synchronised or triggered motion is useful in representing the effect of tokens in Petri nets, in modelling systems in which customers and work can be instantaneously moved from one queue to the other upon certain events, and also for certain behaviours encountered in parallel computer system modelling. We show that this new class of network has product-form stationary solution, and establish the non-linear customer flow equations which govern it. Network stability is discussed in this new context.

A single-server retrial queue consists of a primary queue, an orbit and a single server. Assume the primary queue capacity is 1 and the orbit capacity is infinite. Customers can arrive at the primary queue either from outside the system or from the orbit. If the server is busy, the arriving customer joins the orbit and conducts a retrial later. Otherwise, he receives service and leaves the system.

We investigate the stability condition for a single-server retrial queue. Let λ be the arrival rate and 1/μ be the mean service time. It has been proved that λ/μ < 1 is a sufficient stability condition for the M/G/1/1 retrial queue with exponential retrial times. We give a counterexample to show that this stability condition is not valid for general single-server retrial queues. Next we show that λ /μ < 1 is a sufficient stability condition for the stability of a single-server retrial queue when the interarrival times and retrial times are finite mixtures of Erlangs.

The main objective of this paper is to investigate the conditional behavior of the multivariate reward process given the number of certain signals where the underlying system is described by a semi-Markov process and the signal is defined by a counting process. To this end, we study the joint behavior of the multivariate reward process and the multivariate counting process in detail. We derive transform results as well as the corresponding real domain expressions, thus providing clear probabilistic interpretation.

The steady-state analysis of a quasi-birth-death process is possible by matrix geometric procedures in which the root to a quadratic matrix equation is found. A recent method that can be used for analyzing quasi-birth–death processes involves expanding the state space and using a linear matrix equation instead of the quadratic form. One of the difficulties of using the linear matrix equation approach regards the boundary conditions and obtaining the norming equation. In this paper, we present a method for calculating the boundary values and use the operator-machine interference problem as a vehicle to compare the two approaches for solving quasi-birth-death processes.

Burn-in is a procedure used for eliminating weak components in a mixed population. In this paper we focus on general mixed populations. Three types of results are established. First, it is shown that any mixed population displays a type of monotonicity property which is appropriate for burn-in. Second, it is shown that if, asymptotically, components have constant failure rates, then the mixed population will also asymptotically have a constant failure rate and this will correspond to the rate of the strongest subpopulation of the mixture. Finally, it is shown for a reasonable cost function, that if one mixture distribution dominates another in a strong sense, the resulting mixture of the dominant distribution will have larger optimal burn-in time.

A new approach is used to obtain the transient probabilities of the M/M/1 queueing system. The first step of this approach deals with the generating function of the transient probabilities of the uniformized Markov chain associated with this queue. The second step consists of the inversion of this generating function. A new analytical expression of the transient probabilities of the M/M/1 queue is then obtained.

Continuous-time Markov chain models have been widely considered for the gating behaviour of a single ion channel. In such models the state space is usually partitioned into two classes, designated ‘open' and ‘closed', and there is ‘aggregation' in that it is possible to observe only which class the process is in at any given time. Hawkes et al. (1990) have derived an expression for the density function of the exact distribution of an observed open time in such an aggregated Markov model, where brief sojourns in either the open or the closed class are unobservable. This paper extends their result to single ion channel models based on aggregated semi-Markov processes, giving a more direct derivation which is probabilistic and exhibits clearly the combinatorial content.