Refine listing
Actions for selected content:
1446 results in 60Kxx
Partially observable semi-Markov reward processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 548-560
- Print publication:
- September 1993
-
- Article
- Export citation
Utilization of the method of linear matrix equations to solve a quasi-birth-death problem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 639-649
- Print publication:
- September 1993
-
- Article
- Export citation
Burn-in and mixed populations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 692-702
- Print publication:
- September 1993
-
- Article
- Export citation
Transient analysis of the M/M/1 queue
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 702-713
- Print publication:
- September 1993
-
- Article
- Export citation
On the exact distribution of observed open times in single ion channel models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 529-537
- Print publication:
- September 1993
-
- Article
- Export citation
On zero-avoiding transition probabilities of an r-node tandem queue: a combinatorial approach
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 737-741
- Print publication:
- September 1993
-
- Article
- Export citation
On Klimov's model by two job classes and exponential processing times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 716-724
- Print publication:
- September 1993
-
- Article
- Export citation
Induced rare events: analysis via large deviations and time reversal
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 667-689
- Print publication:
- September 1993
-
- Article
- Export citation
Critical behavior of percolation and Markov fields on branching planes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 538-547
- Print publication:
- September 1993
-
- Article
- Export citation
A logarithmic reduction algorithm for quasi-birth-death processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 650-674
- Print publication:
- September 1993
-
- Article
- Export citation
Transient behavior of coverage processes by applications to the infinite-server queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 589-601
- Print publication:
- September 1993
-
- Article
- Export citation
Superposition of Markov renewal processes and applications
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 585-606
- Print publication:
- September 1993
-
- Article
- Export citation
A two-point Markov chain boundary-value problem
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 607-630
- Print publication:
- September 1993
-
- Article
- Export citation
Insensitivity and product-form decomposability of reallocatable GSMP
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 415-437
- Print publication:
- June 1993
-
- Article
- Export citation
A new look at the Moran dam
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 489-495
- Print publication:
- June 1993
-
- Article
- Export citation
Optimal buffer allocation in a two-stage queueing system
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 478-482
- Print publication:
- June 1993
-
- Article
- Export citation
The transient blocking probabilities in M/M/N loss systems via large deviations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 483-486
- Print publication:
- June 1993
-
- Article
-
- You have access
- Export citation
Point-based polygonal models for random graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 348-372
- Print publication:
- June 1993
-
- Article
- Export citation
The geometricity of the limiting distributions in queues and dams
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 438-445
- Print publication:
- June 1993
-
- Article
- Export citation
The matrix M/M/∞ system: retrial models and Markov Modulated sources
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 453-471
- Print publication:
- June 1993
-
- Article
- Export citation
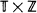 , where
, where 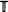 is a homogeneous tree and
is a homogeneous tree and 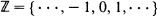 is a one-dimensional lattice, it is shown, by verifying that the triangle condition is satisfied, that the percolation probability
is a one-dimensional lattice, it is shown, by verifying that the triangle condition is satisfied, that the percolation probability 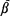 ,
, 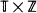 are also obtained.
are also obtained.