Refine listing
Actions for selected content:
1446 results in 60Kxx
Another look at the moment bounds on reliability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 777-787
- Print publication:
- September 1994
-
- Article
- Export citation
Ruin estimation for a general insurance risk model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 404-422
- Print publication:
- June 1994
-
- Article
- Export citation
The Beňes equations for the distribution of excursions for general storage processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 418-429
- Print publication:
- June 1994
-
- Article
- Export citation
Sensitivity analysis for stationary and ergodic queues: additional results
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 556-560
- Print publication:
- June 1994
-
- Article
- Export citation
On the mean sojourn time of jobs in queues by general service disciplines
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 516-538
- Print publication:
- June 1994
-
- Article
- Export citation
Sur une procédure de branchement déterministe et ses dérivées aléatoires
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 333-347
- Print publication:
- June 1994
-
- Article
- Export citation
On maintained systems operating in a random environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 589-594
- Print publication:
- June 1994
-
- Article
- Export citation
Preservation of certain classes of life distributions under Poisson shock models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 458-465
- Print publication:
- June 1994
-
- Article
- Export citation
State-dependent signalling in queueing networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 436-455
- Print publication:
- June 1994
-
- Article
- Export citation
Approximating gamma distributions by normalized negative binomial distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 391-400
- Print publication:
- June 1994
-
- Article
- Export citation
A stochastic model of fragment formation when DNA replicates
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 301-308
- Print publication:
- June 1994
-
- Article
- Export citation
GI/G/1 processor sharing queue in heavy traffic
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 539-555
- Print publication:
- June 1994
-
- Article
- Export citation
MR/GI/1 queues by positively correlated arrival stream
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 497-514
- Print publication:
- June 1994
-
- Article
- Export citation
On transient behaviour of a nearest-neighbour birth-death process on a lattice
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 549-553
- Print publication:
- June 1994
-
- Article
- Export citation
On the existence of finite-dimensional filters for Markov-modulated traffic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 515-525
- Print publication:
- June 1994
-
- Article
- Export citation
A Dam with seasonal input
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 526-541
- Print publication:
- June 1994
-
- Article
- Export citation
Loss probabilities in a simple circuit-switched network
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 456-473
- Print publication:
- June 1994
-
- Article
- Export citation
Analysis of the M x/G/1 queue by N-policy and multiple vacations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 476-496
- Print publication:
- June 1994
-
- Article
- Export citation
An application of random packing to the multiple fracture of composite materials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 564-569
- Print publication:
- June 1994
-
- Article
- Export citation
Optimality of the round-robin routing policy
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 466-475
- Print publication:
- June 1994
-
- Article
- Export citation
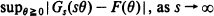 . In particular, we show that the exact order of uniform convergence is
. In particular, we show that the exact order of uniform convergence is 