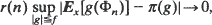Refine listing
Actions for selected content:
1446 results in 60Kxx
Inspection times for stand-by units
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1015-1025
- Print publication:
- December 1994
-
- Article
- Export citation
On the input-output map of a G/G/1 queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1128-1133
- Print publication:
- December 1994
-
- Article
- Export citation
Servers in tandem with k-stage blocking and communications-type flow
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1061-1069
- Print publication:
- December 1994
-
- Article
- Export citation
A new approach to the G/G/1 queue with generalized setup time and exhaustive service
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1083-1097
- Print publication:
- December 1994
-
- Article
- Export citation
A bivariate optimal replacement policy for a repairable system
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1123-1127
- Print publication:
- December 1994
-
- Article
- Export citation
Classes of life distributions and renewal counting process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1110-1115
- Print publication:
- December 1994
-
- Article
- Export citation
A limit theorem for certain disordered random systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1022-1043
- Print publication:
- December 1994
-
- Article
- Export citation
Queueing in space
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1095-1116
- Print publication:
- December 1994
-
- Article
- Export citation
Matrix product-form solutions for Markov chains with a tree structure
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 965-987
- Print publication:
- December 1994
-
- Article
- Export citation
A sample path approach to mean busy periods for Markov-modulated queues and fluids
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1117-1121
- Print publication:
- December 1994
-
- Article
-
- You have access
- Export citation
A note on the existence of regeneration times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1116-1122
- Print publication:
- December 1994
-
- Article
- Export citation
Exponential upper bounds via martingales for multiplexers with Markovian arrivals
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1049-1060
- Print publication:
- December 1994
-
- Article
- Export citation
Maximization of a survival probability and its application
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1026-1033
- Print publication:
- December 1994
-
- Article
- Export citation
Semi-Markov Replacement Chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 728-755
- Print publication:
- September 1994
-
- Article
- Export citation
Regenerative rare events simulation via likelihood ratios
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 797-815
- Print publication:
- September 1994
-
- Article
- Export citation
Ergodicity of a Jackson network by batch arrivals
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 847-853
- Print publication:
- September 1994
-
- Article
- Export citation
Transient solutions for denumerable-state Markov processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 635-645
- Print publication:
- September 1994
-
- Article
- Export citation
Subgeometric Rates of Convergence of f-Ergodic Markov Chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 26 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 01 July 2016, pp. 775-798
- Print publication:
- September 1994
-
- Article
- Export citation
Lundberg bounds on the tails of compound distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 743-756
- Print publication:
- September 1994
-
- Article
- Export citation
The Mk/G/∞ batch arrival queue by heterogeneous dependent demands
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 841-846
- Print publication:
- September 1994
-
- Article
- Export citation
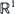 :
: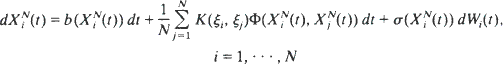
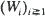 is a sequence of independent copies of the one-dimensional Brownian motion
is a sequence of independent copies of the one-dimensional Brownian motion 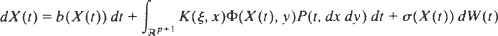
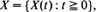 , the existence of a first regeneration time,
, the existence of a first regeneration time, 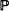 [queue length
[queue length 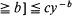 for any
for any 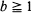 where
where