Refine listing
Actions for selected content:
1446 results in 60Kxx
Queues with marked customers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 567-587
- Print publication:
- June 1996
-
- Article
- Export citation
The M/G/1 queue with negative customers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 540-566
- Print publication:
- June 1996
-
- Article
- Export citation
Symmetric queues with batch departures and their networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 308-326
- Print publication:
- March 1996
-
- Article
- Export citation
Spectral analysis of M/G/1 and G/M/1 type Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 114-165
- Print publication:
- March 1996
-
- Article
- Export citation
Tail of compound distributions and excess time
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 184-195
- Print publication:
- March 1996
-
- Article
- Export citation
Large deviations for discrete and continuous percolation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 29-52
- Print publication:
- March 1996
-
- Article
- Export citation
Expansions for Markov-modulated systems and approximations of ruin probability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 57-70
- Print publication:
- March 1996
-
- Article
- Export citation
Asymptotic analysis of queueing systems with identical service
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 267-281
- Print publication:
- March 1996
-
- Article
- Export citation
A non-exponential generalization of an inequality arising in queueing and insurance risk
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 176-183
- Print publication:
- March 1996
-
- Article
- Export citation
A sample path analysis of the delay in the M/G/C system
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 256-266
- Print publication:
- March 1996
-
- Article
- Export citation
Increasing the reliability of a machine reduces the period of its work
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 217-223
- Print publication:
- March 1996
-
- Article
- Export citation
On coupling of random walks and renewal processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 122-126
- Print publication:
- March 1996
-
- Article
- Export citation
Performance analysis of the discrete-time GI/Geom/1/N queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 239-255
- Print publication:
- March 1996
-
- Article
- Export citation
A heterogeneous blocking system in a random environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 211-216
- Print publication:
- March 1996
-
- Article
- Export citation
Asymptotic distribution theory for Hoare's selection algorithm
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 252-269
- Print publication:
- March 1996
-
- Article
- Export citation
On stochastic ordering of random vectors
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 960-965
- Print publication:
- December 1995
-
- Article
- Export citation
Markov-modulated traffic with nearly complete decomposability characteristics and associated fluid queueing models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1144-1185
- Print publication:
- December 1995
-
- Article
- Export citation
On the HNBUE property in a class of correlated cumulative shock models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1186-1188
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
Probability bounds on the finite sum of the binary sequence of order k
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1014-1027
- Print publication:
- December 1995
-
- Article
- Export citation
Comparison of replacement policies via point processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1079-1103
- Print publication:
- December 1995
-
- Article
- Export citation
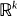 can be made such that S' — S is virtually a one-dimensional simple random walk. This insight settles a zero-two law of ergodicity. One more proof of Blackwell's renewal theorem is also presented.
can be made such that S' — S is virtually a one-dimensional simple random walk. This insight settles a zero-two law of ergodicity. One more proof of Blackwell's renewal theorem is also presented.