Refine listing
Actions for selected content:
1446 results in 60Kxx
A local proof of the Swiss Army formula of Palm calculus
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 909-914
- Print publication:
- September 1996
-
- Article
- Export citation
Stability of feed-forward fluid networks with Lévy input
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 513-522
- Print publication:
- September 1996
-
- Article
- Export citation
Strong approximations for some open population epidemic models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 448-457
- Print publication:
- September 1996
-
- Article
- Export citation
The stability of storage models with shot noise input
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 830-839
- Print publication:
- September 1996
-
- Article
- Export citation
General conditions for bounded relative error in simulations of highly reliable Markovian systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 687-727
- Print publication:
- September 1996
-
- Article
- Export citation
A general formula for the downtime distribution of a parallel system
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 772-785
- Print publication:
- September 1996
-
- Article
- Export citation
Heavy traffic analysis of a transportation network model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 870-885
- Print publication:
- September 1996
-
- Article
- Export citation
An infinite variance solidarity theorem for Markov renewal functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 434-438
- Print publication:
- September 1996
-
- Article
- Export citation
From FIFO to LIFO: a functional ordering of service delay via arrival discipline
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 507-512
- Print publication:
- September 1996
-
- Article
- Export citation
Continuity of percolation probability in ∞ + 1 dimensions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 427-433
- Print publication:
- September 1996
-
- Article
- Export citation
On closure of some partial orderings under mixtures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 698-706
- Print publication:
- September 1996
-
- Article
- Export citation
Economies of scale in queues with sources having power-law large deviation scalings
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 840-857
- Print publication:
- September 1996
-
- Article
- Export citation
On heavy traffic approximations for transient characteristics of M/M/∞ queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 490-506
- Print publication:
- September 1996
-
- Article
- Export citation
Networks of queues with batch services and customer coalescence
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 858-869
- Print publication:
- September 1996
-
- Article
- Export citation
Busy period in GIX/G/∞
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 815-829
- Print publication:
- September 1996
-
- Article
- Export citation
Rate modulation in dams and ruin problems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 523-535
- Print publication:
- September 1996
-
- Article
- Export citation
A note on disjoint-occurrence inequalities for marked Poisson point processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 420-426
- Print publication:
- September 1996
-
- Article
- Export citation
A modified block replacement policy with two variables and general random minimal repair cost
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 557-572
- Print publication:
- September 1996
-
- Article
- Export citation
On a Markov chain approach for the study of reliability structures
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 357-367
- Print publication:
- September 1996
-
- Article
- Export citation
A unified method to analyze overtake free queueing systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 588-625
- Print publication:
- June 1996
-
- Article
- Export citation
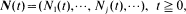 , be a recurrent Markov renewal process and
, be a recurrent Markov renewal process and 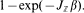 . Let
. Let 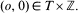 . Denote by
. Denote by 