Refine listing
Actions for selected content:
1446 results in 60Kxx
The propagation of chaos of multitype mean field interacting particle systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 346-362
- Print publication:
- June 1997
-
- Article
- Export citation
Stochastic comparisons of random minima and maxima
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 420-425
- Print publication:
- June 1997
-
- Article
- Export citation
Sur Une Équation Fonctionnelle Et SES Applications: Une Extension Du Théorème De Kesten-Stigum Concernant Des Processus De Branchement
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 353-373
- Print publication:
- June 1997
-
- Article
- Export citation
Large deviations of heavy-tailed random sums with applications in insurance and finance
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 293-308
- Print publication:
- June 1997
-
- Article
- Export citation
A Geometric Product-Form Distribution for a Queueing Network by Non-Standard Batch Arrivals and Batch Transfers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 523-544
- Print publication:
- June 1997
-
- Article
- Export citation
Stochastic orders based on ratios of Laplace transforms
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 404-419
- Print publication:
- June 1997
-
- Article
- Export citation
Unification of Software Reliability Models by Self-Exciting Point Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 337-352
- Print publication:
- June 1997
-
- Article
- Export citation
Smoothed Perturbation Analysis for Single-Server Queues by Some General Service Disciplines
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 545-566
- Print publication:
- June 1997
-
- Article
- Export citation
Reliability analysis of M/G/1 queueing systems with server breakdowns and vacations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 546-555
- Print publication:
- June 1997
-
- Article
- Export citation
A perpetuity and the M/M/∞ ranked server system
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 508-513
- Print publication:
- June 1997
-
- Article
- Export citation
Stochastic comparisons for fork-join queues with exponential processing times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 487-497
- Print publication:
- June 1997
-
- Article
- Export citation
Stochastic storage networks: stationarity and the feedforward case
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 498-507
- Print publication:
- June 1997
-
- Article
- Export citation
A note on single server loss systems with a superposition of inputs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 213-222
- Print publication:
- March 1997
-
- Article
- Export citation
Variants of the Choquet–Deny theorem with applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 101-106
- Print publication:
- March 1997
-
- Article
- Export citation
Superposition of Interacting Aggregated Continuous-Time Markov Chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 56-91
- Print publication:
- March 1997
-
- Article
- Export citation
A correspondence between product-form batch-movement queueing networks and single-movement networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 160-175
- Print publication:
- March 1997
-
- Article
- Export citation
Explicit solution of an optimal stopping problem: the burn-in of conditionally exponential components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 267-282
- Print publication:
- March 1997
-
- Article
- Export citation
Ageing first-passage times of Markov processes: a matrix approach
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-13
- Print publication:
- March 1997
-
- Article
- Export citation
Stationary M/G/1 excursions in the presence of heavy tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 208-212
- Print publication:
- March 1997
-
- Article
- Export citation
Steady state solution of a single-server queue with linear repeated requests
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 223-233
- Print publication:
- March 1997
-
- Article
- Export citation
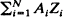 , where {Z
, where {Z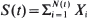 ,
, 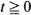 , where
, where 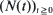 are non-negative integer-valued random variables and are
are non-negative integer-valued random variables and are 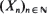 i.i.d. non-negative random variables with common distribution function
i.i.d. non-negative random variables with common distribution function 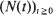 . Special attention is paid to the compound Poisson process and its ramifications. The right tail of the distribution function
. Special attention is paid to the compound Poisson process and its ramifications. The right tail of the distribution function 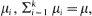 , where
, where 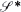 of subexponential distributions are asymptotically of two types as
of subexponential distributions are asymptotically of two types as 