Refine listing
Actions for selected content:
1446 results in 60Kxx
AB percolation on bond-decorated graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 153-166
- Print publication:
- March 1993
-
- Article
- Export citation
Asymptotic stationarity of multichannel queues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 203-220
- Print publication:
- March 1993
-
- Article
- Export citation
Random splittings of an interval
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 131-152
- Print publication:
- March 1993
-
- Article
- Export citation
Networks and dynamical systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 140-175
- Print publication:
- March 1993
-
- Article
- Export citation
An unusual stochastic order relation with some applications in sampling and epidemic theory
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 25 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 01 July 2016, pp. 63-81
- Print publication:
- March 1993
-
- Article
- Export citation
On a new formula for the transient state probabilities for M/M/1 queues and computational implications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 237-246
- Print publication:
- March 1993
-
- Article
- Export citation
Asymptotic variance parameters for the boundary local times of reflected Brownian motion on a compact interval
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 996-1002
- Print publication:
- December 1992
-
- Article
- Export citation
Some results on block replacement policies and renewal theory
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 932-946
- Print publication:
- December 1992
-
- Article
- Export citation
Evaluation of the decay parameter for some specialized birth-death processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 781-791
- Print publication:
- December 1992
-
- Article
- Export citation
A simple coupling of renewal processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1010-1011
- Print publication:
- December 1992
-
- Article
-
- You have access
- Export citation
Extremal properties of the FIFO discipline in queueing networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 967-978
- Print publication:
- December 1992
-
- Article
- Export citation
Stochastic comparisons for queueing models via random sums and intervals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 960-985
- Print publication:
- December 1992
-
- Article
- Export citation
On closed ring queueing networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 979-995
- Print publication:
- December 1992
-
- Article
- Export citation
Two parallel processors with coupled inputs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 986-1007
- Print publication:
- December 1992
-
- Article
- Export citation
Optimal allocation of resources to nodes of parallel and series systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 894-914
- Print publication:
- December 1992
-
- Article
- Export citation
Multivariate imperfect repair
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 947-956
- Print publication:
- December 1992
-
- Article
- Export citation
Connecting internally balanced quasi-reversible Markov processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 934-959
- Print publication:
- December 1992
-
- Article
- Export citation
An insensitivity property of ladder height distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 616-624
- Print publication:
- September 1992
-
- Article
- Export citation
Analyticity of Poisson-driven stochastic systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 532-541
- Print publication:
- September 1992
-
- Article
- Export citation
Sensitivity analysis for stationary and ergodic queues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 738-750
- Print publication:
- September 1992
-
- Article
- Export citation
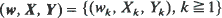 where
where 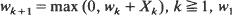 is a vector in
is a vector in 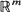 with non-negative coordinates,
with non-negative coordinates, 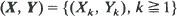 is an
is an 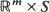 -valued process,
-valued process, 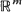 are meant in the coordinate-wise sense. It is shown that a type of asymptotic stationarity of (
are meant in the coordinate-wise sense. It is shown that a type of asymptotic stationarity of (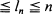 we find a necessary and sufficient condition on {
we find a necessary and sufficient condition on {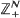 or Markovian models for queueing networks with identical customers is introduced. It is based on the analysis of the intrinsic dynamical system associated with the random walk. Earlier results for small dimensions are presented from this novel point of view. We give proofs of new results for higher dimensions related to the existence of a continuous invariant measure for the underlying dynamical system. Two constants are shown to be important: the free energy
or Markovian models for queueing networks with identical customers is introduced. It is based on the analysis of the intrinsic dynamical system associated with the random walk. Earlier results for small dimensions are presented from this novel point of view. We give proofs of new results for higher dimensions related to the existence of a continuous invariant measure for the underlying dynamical system. Two constants are shown to be important: the free energy  -valued random variables, unusual in the literature, based on the descending factorial moments. Further applications of the ordering occur when comparing certain sampling procedures through the number of un-sampled individuals. In particular, it is used to reinforce slightly comparison results obtained earlier for two such samplings.
-valued random variables, unusual in the literature, based on the descending factorial moments. Further applications of the ordering occur when comparing certain sampling procedures through the number of un-sampled individuals. In particular, it is used to reinforce slightly comparison results obtained earlier for two such samplings.