Refine listing
Actions for selected content:
1446 results in 60Kxx
The Mk /M/∞ queue with heterogeneous customers in a batch
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 477-481
- Print publication:
- June 1992
-
- Article
- Export citation
On the weak convergence of sequences of circuit processes: a probabilistic approach
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 374-383
- Print publication:
- June 1992
-
- Article
- Export citation
Generalised eigenproblems arising in aggregated markov processes allowing for time interval omission
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 302-321
- Print publication:
- June 1992
-
- Article
- Export citation
Time-dependent process of M/G/1 vacation models with exhaustive service
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 418-429
- Print publication:
- June 1992
-
- Article
- Export citation
A central limit theorem by remainder term for renewal processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 267-287
- Print publication:
- June 1992
-
- Article
- Export citation
Some notes on two types of minimal repair
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 226-228
- Print publication:
- March 1992
-
- Article
-
- You have access
- Export citation
Asymptotic reliability of consecutive k-out-of-n systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 142-155
- Print publication:
- March 1992
-
- Article
- Export citation
Limit theorem and large deviation principle for the Voronoi tessellation generated by a Gibbs point process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 45-70
- Print publication:
- March 1992
-
- Article
- Export citation
Unilateral Gaussian fields
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 95-112
- Print publication:
- March 1992
-
- Article
- Export citation
New better than used in expectation processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 116-128
- Print publication:
- March 1992
-
- Article
- Export citation
LRU is better than FIFO under the independent reference model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 239-243
- Print publication:
- March 1992
-
- Article
- Export citation
Light traffic approximations in many-server queues
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 202-218
- Print publication:
- March 1992
-
- Article
- Export citation
The MacLaurin series for the GI/G/1 queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 176-184
- Print publication:
- March 1992
-
- Article
- Export citation
On the probability that the kth customer finds an M/M/1 queue empty
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 238-239
- Print publication:
- March 1992
-
- Article
-
- You have access
- Export citation
Rare events in series of queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 168-175
- Print publication:
- March 1992
-
- Article
- Export citation
Limit distributions of maximal segmental score among Markov-dependent partial sums
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 113-140
- Print publication:
- March 1992
-
- Article
- Export citation
Exact distribution theory for some point process record models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 20-44
- Print publication:
- March 1992
-
- Article
- Export citation
The efficiency and heavy traffic properties of the score function method in sensitivity analysis of queueing models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 172-201
- Print publication:
- March 1992
-
- Article
- Export citation
Discrete-time queueing networks with geometric release probabilities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 24 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 01 July 2016, pp. 229-233
- Print publication:
- March 1992
-
- Article
-
- You have access
- Export citation
Stochastic convexity of sums of i.i.d. non-negative random variables with applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 156-167
- Print publication:
- March 1992
-
- Article
- Export citation
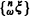 whose finite distributions depend upon the sample paths
whose finite distributions depend upon the sample paths 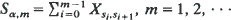 is determined by a realization
is determined by a realization 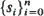 of states with s
of states with s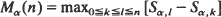 is derived. Computational methods with potential applications to the analysis of random Markov-dependent letter sequences (e.g. DNA and protein sequences) are presented.
is derived. Computational methods with potential applications to the analysis of random Markov-dependent letter sequences (e.g. DNA and protein sequences) are presented.