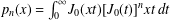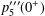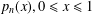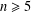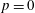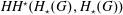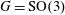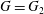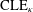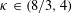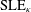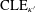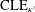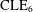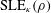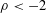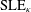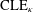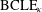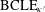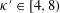Refine listing
Actions for selected content:
38 results in 81Txx
ON BORWEIN’S CONJECTURES FOR PLANAR UNIFORM RANDOM WALKS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 09 October 2019, pp. 392-411
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
The Batalin–Vilkovisky Algebra in the String Topology of Classifying Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 843-889
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
A NOTE ON GUNNINGHAM’S FORMULA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 389-401
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
CLE PERCOLATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 5 / 2017
- Published online by Cambridge University Press:
- 03 October 2017, e4
-
- Article
-
- You have access
- Open access
- Export citation
PyCFTBoot: A Flexible Interface for the Conformal Bootstrap
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 1 / July 2017
- Published online by Cambridge University Press:
- 03 May 2017, pp. 1-38
- Print publication:
- July 2017
-
- Article
- Export citation
DUBROVIN’S SUPERPOTENTIAL AS A GLOBAL SPECTRAL CURVE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 17 April 2017, pp. 449-497
- Print publication:
- May 2019
-
- Article
- Export citation
Lattice Boltzmann Simulation of Steady Flow in a Semi-Elliptical Cavity
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 07 February 2017, pp. 692-717
- Print publication:
- March 2017
-
- Article
- Export citation
Homogeneity of cohomology classes associated with Koszul matrix factorizations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 10 / October 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 2071-2112
- Print publication:
- October 2016
-
- Article
- Export citation
A Feynman integral via higher normal functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 12 / December 2015
- Published online by Cambridge University Press:
- 06 August 2015, pp. 2329-2375
- Print publication:
- December 2015
-
- Article
- Export citation
SOBOLEV SPACES ON LOCALLY COMPACT ABELIAN GROUPS AND THE BOSONIC STRING EQUATION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 39-53
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
Massless Wigner particles in conformal field theory are free
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 22 August 2014, e21
-
- Article
-
- You have access
- Open access
- Export citation
CONSTRUCTION OF TWO-DIMENSIONAL QUANTUM FIELD MODELS THROUGH LONGO–WITTEN ENDOMORPHISMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 10 April 2014, e7
-
- Article
-
- You have access
- Open access
- Export citation
Instantons beyond topological theory. I
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 3 / July 2011
- Published online by Cambridge University Press:
- 12 May 2011, pp. 463-565
- Print publication:
- July 2011
-
- Article
- Export citation
SOME C*-ALGEBRAS ASSOCIATED TO QUANTUM GAUGE THEORIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 18 May 2011, pp. 9-24
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
LOOP GROUPS, STRING CLASSES AND EQUIVARIANT COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 22 March 2011, pp. 109-127
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
GEOMETRIC AND TOPOLOGICAL STRUCTURES RELATED TO M-BRANES II: TWISTED STRING AND STRINGC STRUCTURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 09 June 2011, pp. 93-108
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
Supersymmetry of the chiral de Rham complex
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 503-521
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Multipartitions, generalized Durfee squares and affine Lie algebra characters
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 01 August 2017, pp. 395-408
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation