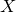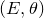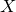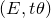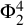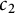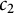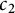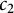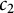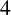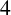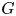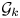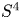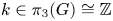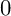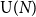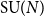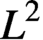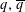Refine listing
Actions for selected content:
38 results in 81Txx
Quantum K theory of Grassmannians, Wilson line operators and Schur bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 04 September 2025, e140
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The algebraic structure of Dyson–Schwinger equations with multiple insertion places
- Part of
-
- Journal:
- Canadian Mathematical Communications / Volume 1 / 2025
- Published online by Cambridge University Press:
- 29 August 2025, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local topological order and boundary algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 August 2025, e135
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A bialgebra theory of Gel’fand-Dorfman algebras with applications to Lie conformal bialgebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 11 July 2025, pp. 1-33
-
- Article
- Export citation
Asymptotic behaviour of large-scale solutions of Hitchin’s equations in higher rank
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large N limit of the Yang–Mills measure on compact surfaces II: Makeenko–Migdal equations and the planar master field
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 January 2025, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUPLED FREE FERMION CONFORMAL FIELD THEORY AND REPRESENTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 15 April 2024, p. 170
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
A remark on Gibbs measures with log-correlated Gaussian fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 April 2024, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A result on the
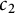 $c_2$ invariant for powers of primes
$c_2$ invariant for powers of primes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1164-1178
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NEW HIGHER ORDER YANG–MILLS–HIGGS FLOW ON RIEMANNIAN
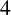 $4$-MANIFOLDS
$4$-MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 29 November 2022, pp. 320-329
- Print publication:
- April 2023
-
- Article
- Export citation
The mod-p homology of the classifying spaces of certain gauge groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 19 September 2022, pp. 1805-1817
- Print publication:
- December 2023
-
- Article
- Export citation
SOLUTIONS OF THE tt*-TODA EQUATIONS AND QUANTUM COHOMOLOGY OF MINUSCULE FLAG MANIFOLDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 10 June 2022, pp. 990-1004
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TAMARKIN–TSYGAN CALCULUS AND CHIRAL POISSON COHOMOLOGY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 751-765
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Combinatorics of the geometry of Wilson loop diagrams II: Grassmann necklaces, dimensions, and denominators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 23 July 2021, pp. 1625-1672
- Print publication:
- December 2022
-
- Article
- Export citation
Large N behaviour of the two-dimensional Yang–Mills partition function
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 30 June 2021, pp. 144-165
-
- Article
- Export citation
GRADIENT FLOWS OF HIGHER ORDER YANG–MILLS–HIGGS FUNCTIONALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 31 May 2021, pp. 257-287
- Print publication:
- October 2022
-
- Article
- Export citation
Combinatorics of the geometry of Wilson loop diagrams I: equivalence classes via matroids and polytopes
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 1177-1208
- Print publication:
- August 2022
-
- Article
- Export citation
Twisted Donaldson invariants
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 04 February 2021, pp. 515-568
- Print publication:
- November 2021
-
- Article
- Export citation
A CLASS OF NONHOLOMORPHIC MODULAR FORMS II: EQUIVARIANT ITERATED EISENSTEIN INTEGRALS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 28 May 2020, e31
-
- Article
-
- You have access
- Open access
- Export citation
Simple Formulas for Constellations and Bipartite Maps with Prescribed Degrees
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 12 November 2019, pp. 160-176
- Print publication:
- February 2021
-
- Article
- Export citation