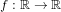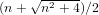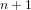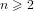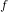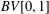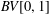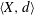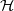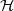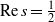Refine listing
Actions for selected content:
154 results in 26-XX
A parallel root-finding algorithm
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 December 2015, pp. 713-729
-
- Article
-
- You have access
- Export citation
On strongly decreasing solutions of cyclic systems of second-order nonlinear differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 5 / October 2015
- Published online by Cambridge University Press:
- 02 September 2015, pp. 1007-1028
- Print publication:
- October 2015
-
- Article
- Export citation
UNIFORMLY BOUNDED COMPOSITION OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 30 July 2015, pp. 463-469
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
LOCAL BOUNDEDNESS OF NONAUTONOMOUS SUPERPOSITION OPERATORS IN
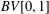 $BV[0,1]$
$BV[0,1]$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 08 July 2015, pp. 325-341
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
Diagonals of Separately Absolutely Continuous Mappings Coincide with the Sums of Absolutely Convergent Series of Continuous Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 10 June 2015, pp. 435-444
-
- Article
- Export citation
MULTIFRACTAL ANALYSIS OF FUNCTIONS ON HEISENBERG AND CARNOT GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 27 March 2015, pp. 1-38
- Print publication:
- February 2017
-
- Article
- Export citation
State-Dependent Fractional Point Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 18-36
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
SOME COMMENTS ON SCALAR DIFFERENTIATION OF VECTOR-VALUED FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 311-321
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
BORNOLOGIES AND LOCALLY LIPSCHITZ FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 15 May 2014, pp. 257-263
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
Fractional Discrete Processes: Compound and Mixed Poisson Representations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 19-36
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
A NEW FORMULA FOR ADOMIAN POLYNOMIALS AND THE ANALYSIS OF ITS TRUNCATED SERIES SOLUTION FOR FRACTIONAL NON-DIFFERENTIABLE INITIAL VALUE PROBLEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 1 / July 2013
- Published online by Cambridge University Press:
- 20 November 2013, pp. 69-92
-
- Article
-
- You have access
- Export citation
ON A QUESTION OF J. M. RASSIAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 27 September 2013, pp. 494-499
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
SYSTEMS OF ISLANDS WITH CONTINUOUS HEIGHT FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 01 May 2013, pp. 385-396
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
COMPLETE MONOTONICITY OF A FUNCTION INVOLVING THE DIVIDED DIFFERENCE OF PSI FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 January 2013, pp. 309-319
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
GENERALISATIONS OF INTEGRAL INEQUALITIES OF HERMITE–HADAMARD TYPE THROUGH CONVEXITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 20 December 2012, pp. 320-330
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
ON THE RANKIN–SELBERG ZETA FUNCTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 101-113
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
ON THE POSITIVITY OF RIEMANN–STIELTJES INTEGRALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 400-405
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
A SOBOLEV ALGEBRA OF VOLTERRA TYPE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 12 December 2012, pp. 313-334
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
ON CONTINUOUS SOLUTIONS OF AN EQUATION OF THE GOŁA̧B–SCHINZEL TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 15 May 2012, pp. 10-17
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
A Fourier Approach for the Level Crossings of Shot Noise Processes with Jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 100-113
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation