Refine listing
Actions for selected content:
154 results in 26-XX
Weighted renewal functions: a hierarchical approach
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 2 / June 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 394-415
- Print publication:
- June 2002
-
- Article
- Export citation
Conditional limit theorems for spectrally positive Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 1 / March 2002
- Published online by Cambridge University Press:
- 19 February 2016, pp. 158-178
- Print publication:
- March 2002
-
- Article
- Export citation
Remarks on converse Carleman and Krein criteria for the classical moment problem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 81-104
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
Shocks, runs and random sums
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 438-448
- Print publication:
- June 2001
-
- Article
- Export citation
Dual characterizations of relative continuity of convex functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 2 / April 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 211-224
- Print publication:
- April 2001
-
- Article
-
- You have access
- Export citation
The number and sum of near-maxima for thin-tailed populations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1100-1116
- Print publication:
- December 2000
-
- Article
- Export citation
Limit theorems for extremes with random sample size
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 777-806
- Print publication:
- September 1998
-
- Article
- Export citation
Generalized regular variation of second order
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 3 / December 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 381-395
- Print publication:
- December 1996
-
- Article
-
- You have access
- Export citation
On the L1-convergence of Fourier transforms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 3 / June 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 405-420
- Print publication:
- June 1996
-
- Article
-
- You have access
- Export citation
Franel integrals of order four
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 2 / April 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 192-203
- Print publication:
- April 1996
-
- Article
-
- You have access
- Export citation
Characterization of upper semicontinuously integrable functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 2 / October 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 244-254
- Print publication:
- October 1995
-
- Article
-
- You have access
- Export citation
Insertion of a measurable function
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 3 / December 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 295-304
- Print publication:
- December 1994
-
- Article
-
- You have access
- Export citation
A sharp inequality related to Moser's inequality
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 357-366
- Print publication:
- December 1993
-
- Article
- Export citation
Limit distributions for compounded sums of extreme order statistics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 557-574
- Print publication:
- September 1992
-
- Article
- Export citation
Concavity and reflected Lévy processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 209-215
- Print publication:
- March 1992
-
- Article
- Export citation
Sharp function estimates for fractional integrals and related operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 1 / August 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-137
- Print publication:
- August 1990
-
- Article
-
- You have access
- Export citation
Ramsey type theorems for real functions
- Part of
-
- Journal:
- Mathematika / Volume 36 / Issue 1 / June 1989
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-141
- Print publication:
- June 1989
-
- Article
- Export citation
Fourier series with small gaps
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 2 / April 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 212-219
- Print publication:
- April 1989
-
- Article
-
- You have access
- Export citation
An extension theorem for convex functions and an application to Teicher's characterization of the normal distribution
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 2 / December 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 155-159
- Print publication:
- December 1987
-
- Article
- Export citation
The multidimensional fundamental theorem of calculus
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 2 / October 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-170
- Print publication:
- October 1987
-
- Article
-
- You have access
- Export citation
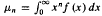 satisfying
satisfying 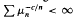 implies that
implies that 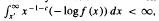
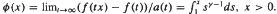 . Then
. Then 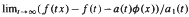 exists non-trivially with a second auxiliary function a
exists non-trivially with a second auxiliary function a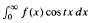 and
and 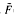 (
(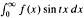 where
where 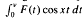 and
and 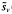
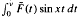 , the modified partial integrals
, the modified partial integrals 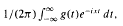 , where
, where 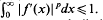 .
.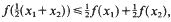
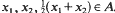 .
. 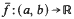
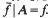 .
.