The purpose of this paper is to study the existence of periodic solutions and the topological structure of the solution set of first-order differential equations involving the distributional Henstock–Kurzweil integral. The distributional Henstock–Kurzweil integral is a general integral, which includes the Lebesgue and Henstock–Kurzweil integrals. The main results extend some previously known results in the literature.

In this paper, using the Schauder Fixed Point Theorem and the Vidossich Theorem, we study the existence of solutions and the structure of the set of solutions of the Darboux problem involving the distributional Henstock–Kurzweil integral. The two theorems presented in this paper are extensions of the previous results of Deblasi and Myjak and of Bugajewski and Szufla.

In this paper we extend some estimates of the right-hand side of a Hermite–Hadamard type inequality for functions whose derivatives’ absolute values are P-convex. Applications to the trapezoidal formula and special means are introduced.

A Chebyshev pseudo-spectral method for solving numerically linear and nonlinear fractional-order integro-differential equations of Volterra type is considered. The fractional derivative is described in the Caputo sense. The suggested method reduces these types of equations to the solution of linear or nonlinear algebraic equations. Special attention is given to study the convergence of the proposed method. Finally, some numerical examples are provided to show that this method is computationally efficient, and a comparison is made with existing results.

The topic of the present paper is a generalized St Petersburg game in which the distribution of the payoff X is given by P(X =sr (k-1)/α) = pq k-1,k = 1, 2,…, where p + q = 1, s = 1 / p,r = 1 / q, and 0 < α ≤ 1. For the case in which α = 1, we extend Feller's classical weak law and Martin-Löf's theorem on convergence in distribution along the 2n -subsequence. The analog for 0 < α < 1 turns out to converge in distribution to an asymmetric stable law with index α. Finally, some limit theorems for polynomial and geometric size total gains, as well as for extremes, are given.

According to the classical Borel lemma, any positive nondecreasing continuous function T satisfiesT(r+1/T(r))≤2T(r) outside a possible exceptional set of finite linear measure. This lemma plays an important role in the theory of entire and meromorphic functions, where the increasing function T is either the logarithm of the maximum modulus function, or the Nevanlinna characteristic. As a result, exceptional sets appear throughout Nevanlinna theory, in particular in Nevanlinna’s second main theorem. In this paper, we consider generalizations of Borel’s lemma. Conversely, we consider ways in which certain inequalities can be modified so as to remove exceptional sets. All results discussed are presented from the point of view of real analysis.

Let β∈(1,2) be a Pisot number and let Hβ denote Garsia’s entropy for the Bernoulli convolution associated with β. Garsia, in 1963, showed that Hβ<1 for any Pisot β. For the Pisot numbers which satisfy xm=xm−1+xm−2+⋯+x+1 (with m≥2), Garsia’s entropy has been evaluated with high precision by Alexander and Zagier for m=2 and later by Grabner, Kirschenhofer and Tichy for m≥3, and it proves to be close to 1. No other numerical values for Hβ are known. In the present paper we show that Hβ>0.81 for all Pisot β, and improve this lower bound for certain ranges of β. Our method is computational in nature.

Zolotarev (1961) proved a duality result that relates stable densities with different indices. In this paper we show how Zolotarev's duality leads to some interesting results on fractional diffusion. Fractional diffusion equations employ fractional derivatives in place of the usual integer-order derivatives. They govern scaling limits of random walk models, with power-law jumps leading to fractional derivatives in space, and power-law waiting times between the jumps leading to fractional derivatives in time. The limit process is a stable Lévy motion that models the jumps, subordinated to an inverse stable process that models the waiting times. Using duality, we relate the density of a spectrally negative stable process with index 1<α<2 to the density of the hitting time of a stable subordinator with index 1/α, and thereby unify some recent results in the literature. These results provide a concrete interpretation of Zolotarev's duality in terms of the fractional diffusion model. They also illuminate a current controversy in hydrology, regarding the appropriate use of space- and time-fractional derivatives to model contaminant transport in river flows.

We introduce a class of stock models that interpolates between exponential Lévy models based on Brownian subordination and certain stochastic volatility models with Lévy-driven volatility, such as the Barndorff-Nielsen–Shephard model. The driving process in our model is a Brownian motion subordinated to a business time which is obtained by convolution of a Lévy subordinator with a deterministic kernel. We motivate several choices of the kernel that lead to volatility clusters while maintaining the sudden extreme movements of the stock. Moreover, we discuss some statistical and path properties of the models, prove absence of arbitrage and incompleteness, and explain how to price vanilla options by simulation and fast Fourier transform methods.

We discuss here the boundedness of the fractional integral operator Iα and its generalized version on generalized nonhomogeneous Morrey spaces. To prove the boundedness of Iα, we employ the boundedness of the so-called maximal fractional integral operator Ia,κ*. In addition, we prove an Olsen-type inequality, which is analogous to that in the case of homogeneous type.

In this paper, a new approach is proposed to investigate Blackwell-type renewal theorems for weighted renewal functions systematically according to which of the tails of weighted renewal constants or the underlying distribution is asymptotically heavier. Some classical results are improved considerably.

A Riesz space-fractional reaction–dispersion equation (RSFRDE) is obtained from the classical reaction–dispersion equation (RDE) by replacing the second-order space derivative with a Riesz derivative of order β∈(1,2]. In this paper, using Laplace and Fourier transforms, we obtain the fundamental solution for a RSFRDE. We propose an explicit finite-difference approximation for a RSFRDE in a bounded spatial domain, and analyse its stability and convergence. Some numerical examples are presented.

Approximations for the Stieltjes integral with (φ,Φ)-Lipschitzian integrators are given. Applications for the Riemann integral of a product and for the generalized trapezoid and Ostrowski inequalities are also provided.

Let F(x ) denote a distribution function in R d and let F *n (x ) denote the nth convolution power of F(x ). In this paper we discuss the asymptotic behaviour of 1 - F *n (x ) as x tends to ∞ in a certain prescribed way. It turns out that in many cases 1 - F *n (x ) ∼ n(1 - F(x )). To obtain results of this type, we introduce and use a form of subexponential behaviour, thereby extending the notion of multivariate regular variation. We also discuss subordination, in which situation the index n is replaced by a random index N.

In this paper, we investigate Volterra spaces and relevant topological properties. New characterizations of weakly Volterra spaces are provided. An analogy of the Banach category theorem in terms of Volterra properties is obtained. It is shown that every weakly Volterra homogeneous space is Volterra, and there are metrizable Baire spaces whose hyperspaces of nonempty compact subsets endowed with the Vietoris topology are not weakly Volterra.

Continuous-time random walks incorporate a random waiting time between random jumps. They are used in physics to model particle motion. A physically realistic rescaling uses two different time scales for the mean waiting time and the deviation from the mean. This paper derives the scaling limits for such processes. These limit processes are governed by fractional partial differential equations that may be useful in physics. A transfer theorem for weak convergence of finite-dimensional distributions of stochastic processes is also obtained.

It is a stylized fact that estimators in extreme-value theory suffer from serious bias. Moreover, graphical representations of extremal data often show erratic behaviour. In the statistical literature it is advised to use a Box–Cox transformation in order to make data more suitable for statistical analysis. We provide some of the theoretical background to see the effect of such transformations and to investigate under what circumstances they might be helpful.

Let X1, X2, …, XN be Banach spaces and ψ a continuous convex function with some appropriate conditions on a certain convex set in RN−1. Let (X1⊕X2⊕…⊕XN)Ψ be the direct sum of X1, X2, …, XN equipped with the norm associated with Ψ. We characterize the strict, uniform, and locally uniform convexity of (X1 ⊕ X2 ⊕ … ⊕ XN)Ψ; by means of the convex function Ψ. As an application these convexities are characterized for the ℓp, q-sum (X1 ⊕ X2 ⊕ … ⊕ XN)p, q (1 < q ≤ p ≤ ∈, q < ∞), which includes the well-known facts for the ℓp-sum (X1 ⊕ X2 ⊕ … ⊕ XN)p in the case p = q.

Let X and Y be separable metrizable spaces, and f: X→Y a function. It is wished to recover f from its values on a small set via a simple algorithm. It is shown that this is possible if f is Baire class one, and in fact a characterization is obtained. This leads to the study of sets of Baire class one functions and to a characterization of the separability of the dual space of an arbitrary Banach space.

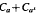In this paper we prove that if a Cantor set has ratios of dissection bounded away from zero, then there is a natural number N, such that its N-fold sum is an interval. Moreover, for each element z of this interval, we explicitly construct the N elements of C whose sum yields z. We also extend a result of Mendes and Oliveria showing that when s is irrational is an interval if and only if a /(1−2a) as/(1−2as) ≥ 1.