Refine listing
Actions for selected content:
154 results in 26-XX
Fast Evaluation of the Caputo Fractional Derivative and its Applications to Fractional Diffusion Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 07 February 2017, pp. 650-678
- Print publication:
- March 2017
-
- Article
- Export citation
Cosine Radial Basis Function Neural Networks for Solving Fractional Differential Equations
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 17 January 2017, pp. 667-679
- Print publication:
- June 2017
-
- Article
- Export citation
A New Family of Difference Schemes for Space Fractional Advection Diffusion Equation
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 282-306
- Print publication:
- April 2017
-
- Article
- Export citation
On the Global Gaussian Lipschitz Space
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 03 January 2017, pp. 707-720
-
- Article
- Export citation
ISOMETRIC REPRESENTATION OF LIPSCHITZ-FREE SPACES OVER CONVEX DOMAINS IN FINITE-DIMENSIONAL SPACES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 538-552
- Print publication:
- 2017
-
- Article
- Export citation
COMPACT SPACES OF THE FIRST BAIRE CLASS THAT HAVE OPEN FINITE DEGREE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 5 / November 2018
- Published online by Cambridge University Press:
- 21 November 2016, pp. 1173-1196
- Print publication:
- November 2018
-
- Article
- Export citation
SHARP INEQUALITIES FOR THE VARIATION OF THE DISCRETE MAXIMAL FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 04 November 2016, pp. 94-107
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
Numerical Solution of Euler-Lagrange Equation with Caputo Derivatives
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 11 October 2016, pp. 173-185
- Print publication:
- February 2017
-
- Article
- Export citation
Multivariate fractional Poisson processes and compound sums
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 691-711
- Print publication:
- September 2016
-
- Article
- Export citation
Jacobi Spectral Collocation Method for the Time Variable-Order Fractional Mobile-Immobile Advection-Dispersion Solute Transport Model
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 337-352
- Print publication:
- August 2016
-
- Article
- Export citation
Stable laws and Beurling kernels
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 239-248
- Print publication:
- July 2016
-
- Article
- Export citation
THE COST–TIME CURVE FOR AN OPTIMAL TRAIN JOURNEY ON LEVEL TRACK
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 01 July 2016, pp. 10-32
-
- Article
-
- You have access
- Export citation
Fischer Decomposition and Cauchy–Kovalevskaya Extension in Fractional Clifford Analysis: The Riemann–Liouville Case
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 251-272
-
- Article
- Export citation
A NEW EXAMPLE OF A DETERMINISTIC CHAOS GAME
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 02 June 2016, pp. 464-470
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Bruckner–Garg-Type Results with Respect to Haar Null Sets in C[0, 1]
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 10 May 2016, pp. 17-30
-
- Article
- Export citation
Multilevel Circulant Preconditioner for High-Dimensional Fractional Diffusion Equations
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 12 May 2016, pp. 109-130
- Print publication:
- May 2016
-
- Article
- Export citation
On a partial theta function and its spectrum
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 19 April 2016, pp. 609-623
- Print publication:
- June 2016
-
- Article
- Export citation
A Second-Order Finite Difference Method for Two-Dimensional Fractional Percolation Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 733-757
- Print publication:
- March 2016
-
- Article
- Export citation
FRACTIONAL MODELS IN SPACE FOR DIFFUSIVE PROCESSES IN HETEROGENEOUS MEDIA WITH APPLICATIONS IN CELL MOTILITY AND ELECTRICAL SIGNAL PROPAGATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 10 February 2016, pp. 518-520
- Print publication:
- June 2016
-
- Article
-
- You have access
- Open access
- Export citation
Exact Solutions for Fractional Differential-Difference Equations by (G'/G)-Expansion Method with Modified Riemann-Liouville Derivative
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 27 January 2016, pp. 293-305
- Print publication:
- April 2016
-
- Article
- Export citation
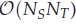 memory and
memory and  work, where
work, where 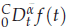 of order
of order 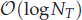 for
for 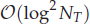 for
for 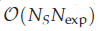 storage and
storage and 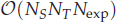 work when numerically solving the time fractional PDEs. Furthermore, we also give the stability and error analysis of the new scheme, and present several numerical examples to demonstrate the performance of our scheme.
work when numerically solving the time fractional PDEs. Furthermore, we also give the stability and error analysis of the new scheme, and present several numerical examples to demonstrate the performance of our scheme.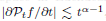 , where
, where 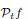 is the Poisson integral of the function
is the Poisson integral of the function 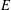
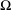
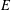
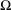
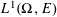
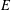


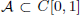 is
is 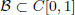 and a Borel probability measure
and a Borel probability measure 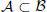 and
and 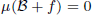 for all
for all 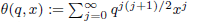 defines a
defines a 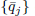 of values of
of values of 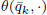 has a double real zero
has a double real zero 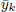 (the rest of its real zeros being simple). For
(the rest of its real zeros being simple). For 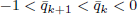 . One has
. One has 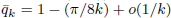 and
and 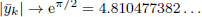 .
.