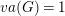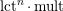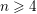Refine listing
Actions for selected content:
62 results in 32Qxx
Second-order estimates for collapsed limits of Ricci-flat Kähler metrics
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 05 January 2023, pp. 912-926
- Print publication:
- September 2023
-
- Article
- Export citation
Pseudo-holomorphic dynamics in the restricted three-body problem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 05 December 2022, pp. 663-693
- Print publication:
- May 2023
-
- Article
- Export citation
Smooth hypersurfaces in abelian varieties over arithmetic rings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 28 October 2022, e97
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
K-stability of Fano varieties via admissible flags
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 30 June 2022, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on holomorphic sectional curvature of a hermitian manifold
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 04 March 2022, pp. 739-745
- Print publication:
- September 2022
-
- Article
- Export citation
Almost existence from the feral perspective and some questions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 792-834
- Print publication:
- February 2022
-
- Article
- Export citation
Uniqueness of optimal symplectic connections
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 04 March 2021, e18
-
- Article
-
- You have access
- Open access
- Export citation
Holomorphic one-forms, fibrations over the circle, and characteristic numbers of Kähler manifolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 95-103
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Minimising CM degree and slope stability of projective varieties
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 February 2021, pp. 125-137
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Lagrangian foliations and Anosov symplectomorphisms on Kähler manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 3325-3335
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
ON THE SHARPNESS OF TIAN’S CRITERION FOR K-STABILITY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 245 / March 2022
- Published online by Cambridge University Press:
- 23 October 2020, pp. 41-73
- Print publication:
- March 2022
-
- Article
- Export citation
Orbifold hyperbolicity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 08 October 2020, pp. 1664-1698
- Print publication:
- August 2020
-
- Article
- Export citation
VIRTUAL ALGEBRAIC FIBRATIONS OF KÄHLER GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 243 / September 2021
- Published online by Cambridge University Press:
- 06 December 2019, pp. 42-60
- Print publication:
- September 2021
-
- Article
- Export citation
K-stability of birationally superrigid Fano varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 9 / September 2019
- Published online by Cambridge University Press:
- 07 August 2019, pp. 1845-1852
- Print publication:
- September 2019
-
- Article
- Export citation
Cross-sections of unknotted ribbon disks and algebraic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 2 / February 2019
- Published online by Cambridge University Press:
- 11 February 2019, pp. 413-423
- Print publication:
- February 2019
-
- Article
- Export citation
Tits Buildings and K-Stability
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 799-815
-
- Article
- Export citation
The volume of singular Kähler–Einstein Fano varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 29 April 2018, pp. 1131-1158
- Print publication:
- June 2018
-
- Article
- Export citation
Del Pezzo Surfaces in Weighted Projective Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 04 April 2018, pp. 545-572
-
- Article
-
- You have access
- Export citation
The Kodaira dimension of complex hyperbolic manifolds with cusps
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 28 November 2017, pp. 549-564
- Print publication:
- March 2018
-
- Article
- Export citation
On the singularity type of full mass currents in big cohomology classes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 2 / February 2018
- Published online by Cambridge University Press:
- 09 November 2017, pp. 380-409
- Print publication:
- February 2018
-
- Article
- Export citation