Refine listing
Actions for selected content:
62 results in 32Qxx
A SCHWARZ LEMMA FOR
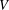 $V$ -HARMONIC MAPS AND THEIR APPLICATIONS
$V$ -HARMONIC MAPS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 17 August 2017, pp. 504-512
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
DIMENSION-FREE UNIFORMITY WITH APPLICATIONS, I
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 734-761
- Print publication:
- 2017
-
- Article
-
- You have access
- HTML
- Export citation
ON INTEGERS OCCURRING AS THE MAPPING DEGREE BETWEEN QUASITORIC 4-MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 23 December 2016, pp. 289-312
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Positivity properties of the bundle of logarithmic tensors on compact Kähler manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 11 / November 2016
- Published online by Cambridge University Press:
- 21 September 2016, pp. 2350-2370
- Print publication:
- November 2016
-
- Article
- Export citation
ON THE EXISTENCE OF A GLOBAL NEIGHBOURHOOD
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 717-726
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
Pseudoholomorphic tori in the Kodaira–Thurston manifold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 12 / December 2015
- Published online by Cambridge University Press:
- 16 July 2015, pp. 2212-2250
- Print publication:
- December 2015
-
- Article
- Export citation
Hilbert–Mumford criterion for nodal curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 10 June 2015, pp. 2076-2130
- Print publication:
- November 2015
-
- Article
- Export citation
Log Canonical Thresholds of Complete Intersection Log Del Pezzo Surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 20 February 2015, pp. 445-483
-
- Article
-
- You have access
- Export citation
Holomorphic Line Bundles Over Domains in Cousin Groups and the Algebraic Dimension of Oeljeklaus-Toma Manifolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 12 December 2014, pp. 273-285
-
- Article
-
- You have access
- Export citation
Représentations linéaires des groupes kählériens : factorisations et conjecture de Shafarevich linéaire
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 26 November 2014, pp. 351-376
- Print publication:
- February 2015
-
- Article
- Export citation
EXPECTED TOPOLOGY OF RANDOM REAL ALGEBRAIC SUBMANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 12 May 2014, pp. 673-702
- Print publication:
- October 2015
-
- Article
- Export citation
Poincaré–Lelong equation via the Hodge–Laplace heat equation
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 11 / November 2013
- Published online by Cambridge University Press:
- 09 September 2013, pp. 1856-1870
- Print publication:
- November 2013
-
- Article
- Export citation
A defect relation for meromorphic maps on generalized p-parabolic manifolds intersecting hypersurfaces in complex projective algebraic varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 21 March 2013, pp. 551-574
-
- Article
-
- You have access
- Export citation
The Hodge ring of Kähler manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 28 February 2013, pp. 637-657
- Print publication:
- April 2013
-
- Article
- Export citation
Test configurations and Okounkov bodies
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 11 October 2012, pp. 1736-1756
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
Castelnuovo bounds for higher-dimensional varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 09 July 2012, pp. 1085-1132
- Print publication:
- July 2012
-
- Article
-
- You have access
- Export citation
Bergman metrics and geodesics in the space of Kähler metrics on principally polarized abelian varieties
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 21 June 2011, pp. 1-25
- Print publication:
- January 2012
-
- Article
- Export citation
Generalizations of Clausen's Formula and algebraic transformations of Calabi–Yau differential equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 30 March 2011, pp. 273-295
-
- Article
-
- You have access
- Export citation
Complex submanifolds, connections and asymptotics
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 373-383
-
- Article
-
- You have access
- Export citation
The General Definition of the Complex Monge–Ampère Operator on Compact Kähler Manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 218-239
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
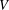
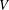
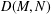
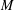
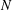
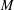
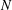
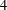
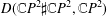
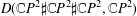
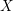
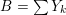
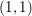
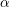
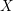
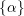
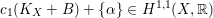
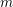
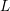
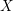
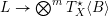
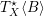
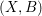
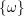
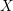
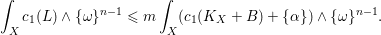
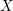
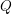
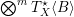
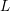
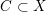
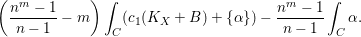



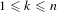
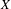
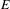

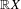
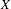

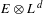
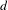
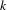

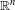
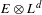


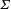
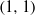
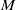
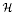 of smooth Kähler metrics in a fixed Kähler class on a polarized Kähler manifold is well approximated by finite-dimensional submanifolds
of smooth Kähler metrics in a fixed Kähler class on a polarized Kähler manifold is well approximated by finite-dimensional submanifolds 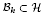 of Bergman metrics of height
of Bergman metrics of height 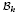 . For any polarized Kähler manifold, the approximation is in the
. For any polarized Kähler manifold, the approximation is in the