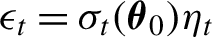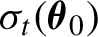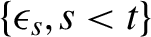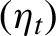Refine search
Actions for selected content:
52379 results in Statistics and Probability
LOCAL ASYMPTOTIC NORMALITY OF GENERAL CONDITIONALLY HETEROSKEDASTIC AND SCORE-DRIVEN TIME-SERIES MODELS
-
- Journal:
- Econometric Theory / Volume 39 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 21 March 2022, pp. 1067-1092
-
- Article
- Export citation
Reflections on a national public health emergency response to carbapenemase-producing Enterobacterales (CPE)
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 18 March 2022, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COVID-19 cases in spectators returning to Finland from UEFA Euro 2020 matches in Saint Petersburg
- Part of
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 18 March 2022, e121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Neonatal cross-infection due to Listeria monocytogenes
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 18 March 2022, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An end-to-end data-driven optimization framework for constrained trajectories
-
- Journal:
- Data-Centric Engineering / Volume 3 / 2022
- Published online by Cambridge University Press:
- 17 March 2022, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Stable Lévy Processes via Lamperti-Type Representations
-
- Published online:
- 16 March 2022
- Print publication:
- 07 April 2022
POST-SELECTION INFERENCE IN THREE-DIMENSIONAL PANEL DATA
-
- Journal:
- Econometric Theory / Volume 39 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 15 March 2022, pp. 623-658
-
- Article
-
- You have access
- Open access
- Export citation
A CROSS-SECTIONAL METHOD FOR RIGHT-TAILED PANIC TESTS UNDER A MODERATELY LOCAL TO UNITY FRAMEWORK
-
- Journal:
- Econometric Theory / Volume 39 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 15 March 2022, pp. 389-411
-
- Article
- Export citation
An adaptive strategy for offering m-out-of-n insurance policies
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 15 March 2022, pp. 106-134
-
- Article
- Export citation
NONPARAMETRIC BAYES ANALYSIS OF THE SHARP AND FUZZY REGRESSION DISCONTINUITY DESIGNS
-
- Journal:
- Econometric Theory / Volume 39 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 15 March 2022, pp. 481-533
-
- Article
- Export citation
An ephemerally self-exciting point process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 14 March 2022, pp. 340-403
- Print publication:
- June 2022
-
- Article
- Export citation
Transmission of COVID-19 among healthcare workers-an epidemiological study during the first phase of the pandemic in Sweden
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 11 March 2022, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal management and valuation of a natural resource: the case of optimal harvesting
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 3 / July 2023
- Published online by Cambridge University Press:
- 11 March 2022, pp. 674-694
-
- Article
- Export citation

Data Visualization for Social and Policy Research
- A Step-by-Step Approach Using R and Python
-
- Published online:
- 10 March 2022
- Print publication:
- 07 April 2022
Fair gambler’s ruin stochastically maximizes playing time
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 10 March 2022, pp. 656-659
- Print publication:
- June 2022
-
- Article
- Export citation
Optimal entry and consumption under habit formation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 10 March 2022, pp. 433-459
- Print publication:
- June 2022
-
- Article
- Export citation
FUNCTIONAL PROFILE TECHNIQUES FOR CLAIMS RESERVING
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 52 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 10 March 2022, pp. 449-482
- Print publication:
- May 2022
-
- Article
- Export citation
Circular specifications and “predicting” with information from the future: Errors in the empirical SAOM–TERGM comparison of Leifeld & Cranmer
-
- Journal:
- Network Science / Volume 10 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 10 March 2022, pp. 3-14
-
- Article
- Export citation
IFoA Presidential Address: “Uncertainty, Culture and Imagination”
-
- Journal:
- British Actuarial Journal / Volume 27 / 2022
- Published online by Cambridge University Press:
- 09 March 2022, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prospective spatial-temporal clusters of COVID-19 in local communities: case study of Kansas City, Missouri, United States
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 09 March 2022, e178
-
- Article
-
- You have access
- Open access
- HTML
- Export citation