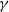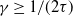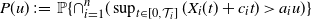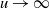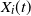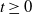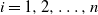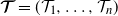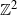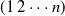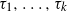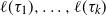Refine search
Actions for selected content:
52379 results in Statistics and Probability
SINR percolation for Cox point processes with random powers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 23 March 2022, pp. 227-253
- Print publication:
- March 2022
-
- Article
- Export citation
Extrema of multi-dimensional Gaussian processes over random intervals
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 81-104
- Print publication:
- March 2022
-
- Article
- Export citation
Epidemiological analysis of rubella-confirmed cases from measles-suspected cases in Ethiopia: threat for congenital rubella syndrome
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 28 February 2022, e55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Epidemiological characteristics in serotype 24 paediatric invasive pneumococcal disease according to an 11-year population-based study in Japan
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 28 February 2022, e66
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mobile Big Data in the fight against COVID-19
-
- Journal:
- Data & Policy / Volume 4 / 2022
- Published online by Cambridge University Press:
- 28 February 2022, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limit theorems and structural properties of the cat-and-mouse Markov chain and its generalisations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 141-166
- Print publication:
- March 2022
-
- Article
- Export citation
Faecal carriage of Clostridioides difficile is low among veterinary healthcare workers in the Netherlands
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 28 February 2022, e63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kingman’s model with random mutation probabilities: convergence and condensation I
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 25 February 2022, pp. 311-335
- Print publication:
- March 2022
-
- Article
- Export citation
Molecular characterization of Chlamydia species in commercial and backyard poultry farms in Costa Rica
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 24 February 2022, e67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fatty acid composition of milk from mothers giving birth at extremely low gestation in Sweden
-
- Journal:
- Experimental Results / Volume 3 / 2022
- Published online by Cambridge University Press:
- 24 February 2022, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Preface
-
- Book:
- Statistical Methods for Climate Scientists
- Published online:
- 03 February 2022
- Print publication:
- 24 February 2022, pp xiii-xviii
-
- Chapter
- Export citation
19 - Extreme Value Theory
-
- Book:
- Statistical Methods for Climate Scientists
- Published online:
- 03 February 2022
- Print publication:
- 24 February 2022, pp 446-467
-
- Chapter
- Export citation
17 - Analysis of Variance and Predictability
-
- Book:
- Statistical Methods for Climate Scientists
- Published online:
- 03 February 2022
- Print publication:
- 24 February 2022, pp 399-417
-
- Chapter
- Export citation
Random stable-type minimal factorizations of the n-cycle
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 24 February 2022, pp. 1-63
- Print publication:
- March 2022
-
- Article
- Export citation
2 - Hypothesis Tests
-
- Book:
- Statistical Methods for Climate Scientists
- Published online:
- 03 February 2022
- Print publication:
- 24 February 2022, pp 30-51
-
- Chapter
- Export citation
1 - Basic Concepts in Probability and Statistics
-
- Book:
- Statistical Methods for Climate Scientists
- Published online:
- 03 February 2022
- Print publication:
- 24 February 2022, pp 1-29
-
- Chapter
- Export citation
13 - Field Significance
-
- Book:
- Statistical Methods for Climate Scientists
- Published online:
- 03 February 2022
- Print publication:
- 24 February 2022, pp 298-313
-
- Chapter
- Export citation
18 - Predictable Component Analysis
-
- Book:
- Statistical Methods for Climate Scientists
- Published online:
- 03 February 2022
- Print publication:
- 24 February 2022, pp 418-445
-
- Chapter
- Export citation
7 - Introduction to Multivariate Methods
-
- Book:
- Statistical Methods for Climate Scientists
- Published online:
- 03 February 2022
- Print publication:
- 24 February 2022, pp 156-184
-
- Chapter
- Export citation
5 - Introduction to Stochastic Processes
-
- Book:
- Statistical Methods for Climate Scientists
- Published online:
- 03 February 2022
- Print publication:
- 24 February 2022, pp 94-125
-
- Chapter
- Export citation