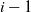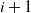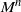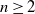Refine search
Actions for selected content:
52379 results in Statistics and Probability
Computing minimal signature of coherent systems through matrix-geometric distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 621-636
- Print publication:
- September 2021
-
- Article
- Export citation
ASB volume 51 issue 3 Cover and Back matter
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 51 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 15 September 2021, pp. b1-b13
- Print publication:
- September 2021
-
- Article
-
- You have access
- Export citation
JPR volume 58 issue 3 Cover and Back matter
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. b1-b2
- Print publication:
- September 2021
-
- Article
-
- You have access
- Export citation
JPR volume 58 issue 3 Cover and Front matter
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. f1-f2
- Print publication:
- September 2021
-
- Article
-
- You have access
- Export citation
Stochastic ordering for birth–death processes with killing
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 708-720
- Print publication:
- September 2021
-
- Article
- Export citation
ASB volume 51 issue 3 Cover and Front matter
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 51 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 15 September 2021, pp. f1-f2
- Print publication:
- September 2021
-
- Article
-
- You have access
- Export citation
On spatial matchings: The first-in-first-match case
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 757-800
- Print publication:
- September 2021
-
- Article
- Export citation
Detailed balance, local detailed balance, and global potential for stochastic chemical reaction networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 886-922
- Print publication:
- September 2021
-
- Article
- Export citation
Stochastic properties of generalized finite mixture models with dependent components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 794-804
- Print publication:
- September 2021
-
- Article
- Export citation
Long range dependence of heavy-tailed random functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 569-593
- Print publication:
- September 2021
-
- Article
- Export citation
On the steady state of continuous-time stochastic opinion dynamics with power-law confidence
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 746-772
- Print publication:
- September 2021
-
- Article
- Export citation
A transient Cramér–Lundberg model with applications to credit risk
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 721-745
- Print publication:
- September 2021
-
- Article
- Export citation
Asymptotic behavior of the weak approximation to a class of Gaussian processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 693-707
- Print publication:
- September 2021
-
- Article
- Export citation
Rejection- and importance-sampling-based perfect simulation for Gibbs hard-sphere models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 839-885
- Print publication:
- September 2021
-
- Article
- Export citation
Variations of the elephant random walk
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 805-829
- Print publication:
- September 2021
-
- Article
- Export citation
Controlled branching processes with continuous time
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 830-848
- Print publication:
- September 2021
-
- Article
- Export citation

Lectures on Random Lozenge Tilings
-
- Published online:
- 31 August 2021
- Print publication:
- 09 September 2021
Associations of genetic variants of miRNA coding regions with pulmonary tuberculosis risk in China
-
- Journal:
- Epidemiology & Infection / Volume 149 / 2021
- Published online by Cambridge University Press:
- 31 August 2021, e208
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On generative models as the basis for digital twins
-
- Journal:
- Data-Centric Engineering / Volume 2 / 2021
- Published online by Cambridge University Press:
- 31 August 2021, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COST-SENSITIVE MULTI-CLASS ADABOOST FOR UNDERSTANDING DRIVING BEHAVIOR BASED ON TELEMATICS
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 51 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 31 August 2021, pp. 719-751
- Print publication:
- September 2021
-
- Article
- Export citation