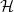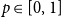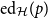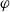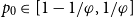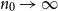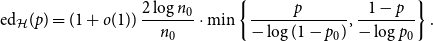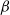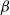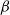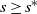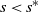Refine search
Actions for selected content:
52379 results in Statistics and Probability
Universal Digital Twin - A Dynamic Knowledge Graph
-
- Journal:
- Data-Centric Engineering / Volume 2 / 2021
- Published online by Cambridge University Press:
- 06 September 2021, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Emulating computer experiments of transport infrastructure slope stability using Gaussian processes and Bayesian inference
-
- Journal:
- Data-Centric Engineering / Volume 2 / 2021
- Published online by Cambridge University Press:
- 06 September 2021, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sub-district level correlation between tuberculosis notifications and socio-demographic factors in Dhaka City corporation, Bangladesh
-
- Journal:
- Epidemiology & Infection / Volume 149 / 2021
- Published online by Cambridge University Press:
- 02 September 2021, e209
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Clinical, health systems and neighbourhood determinants of tuberculosis case fatality in urban Blantyre, Malawi: a multilevel epidemiological analysis of enhanced surveillance data
-
- Journal:
- Epidemiology & Infection / Volume 149 / 2021
- Published online by Cambridge University Press:
- 02 September 2021, e198
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the edit distance function of the random graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 02 September 2021, pp. 345-367
-
- Article
- Export citation
Abattoir-based study of Salmonella prevalence in pigs at slaughter in Great Britain
-
- Journal:
- Epidemiology & Infection / Volume 149 / 2021
- Published online by Cambridge University Press:
- 02 September 2021, e218
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-Gaussian fluctuations of randomly trapped random walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 801-838
- Print publication:
- September 2021
-
- Article
- Export citation
Pathwise large deviations for the rough Bergomi model: Corrigendum
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 849-850
- Print publication:
- September 2021
-
- Article
-
- You have access
- HTML
- Export citation
On the comparison of Shapley values for variance and standard deviation games
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 609-620
- Print publication:
- September 2021
-
- Article
- Export citation
APR volume 53 issue 3 Cover and Back matter
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. b1-b2
- Print publication:
- September 2021
-
- Article
-
- You have access
- Export citation
Estimating tails of independently stopped random walks using concave approximations of hazard functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 773-793
- Print publication:
- September 2021
-
- Article
- Export citation
Subgeometric ergodicity and β-mixing
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 594-608
- Print publication:
- September 2021
-
- Article
- Export citation
APR volume 53 issue 3 Cover and Front matter
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. f1-f2
- Print publication:
- September 2021
-
- Article
-
- You have access
- Export citation
Variational inference for Markovian queueing networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 687-715
- Print publication:
- September 2021
-
- Article
-
- You have access
- HTML
- Export citation
Extinction time of the logistic process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 637-676
- Print publication:
- September 2021
-
- Article
- Export citation
An upper bound for the bond percolation threshold of the cubic lattice by a growth process approach
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 677-692
- Print publication:
- September 2021
-
- Article
- Export citation
Yaglom limit for stochastic fluid models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 649-686
- Print publication:
- September 2021
-
- Article
- Export citation
A regret lower bound for assortment optimization under the capacitated MNL model with arbitrary revenue parameters
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 4 / October 2022
- Published online by Cambridge University Press:
- 01 September 2021, pp. 1266-1274
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Avalanches in a short-memory excitable network
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 609-648
- Print publication:
- September 2021
-
- Article
- Export citation
Diffusion approximation of multi-class Hawkes processes: Theoretical and numerical analysis
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 716-756
- Print publication:
- September 2021
-
- Article
- Export citation