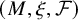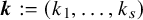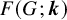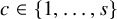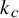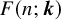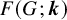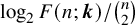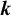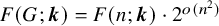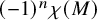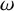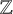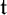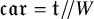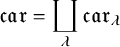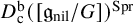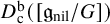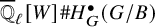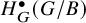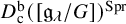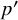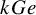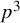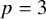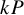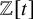866 results in Forum of Mathematics, Sigma
Bordered Floer homology and contact structures
- Part of:
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 14 April 2023, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Grassmanniennes affines tordues sur les entiers – CORRIGENDUM
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 11 April 2023, e28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wonderful compactifications and rational curves with cyclic action
- Part of:
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 11 April 2023, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A generalization of Kruskal’s theorem on tensor decomposition
- Part of:
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 April 2023, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Biharmonic almost complex structures
- Part of:
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 March 2023, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability for the Erdős-Rothschild problem
- Part of:
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 March 2023, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An extension of Venkatesh’s converse theorem to the Selberg class
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 March 2023, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal Euler characteristics for even-dimensional manifolds with finite fundamental group
- Part of:
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 March 2023, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Negative moments of orthogonal polynomials
- Part of:
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 29 March 2023, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extremal Gromov-Witten invariants of the Hilbert scheme of
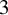 $3$ Points
$3$ Points
- Part of:
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 March 2023, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approximate and discrete Euclidean vector bundles
- Part of:
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 21 March 2023, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On
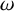 $\omega $-Strongly Measurable Cardinals
$\omega $-Strongly Measurable Cardinals
- Part of:
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 15 March 2023, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Albert algebras over
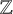 $\mathbb {Z}$ and other rings
$\mathbb {Z}$ and other rings
- Part of:
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 14 March 2023, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global Asymptotics of the Sixth Painlevé Equation in Okamoto’s Space
- Part of:
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 13 March 2023, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the derived Lusztig correspondence
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 07 March 2023, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Decompositions of moduli spaces of vector bundles and graph potentials
- Part of:
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 07 March 2023, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Heights on stacks and a generalized Batyrev–Manin–Malle conjecture
- Part of:
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 March 2023, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structure of blocks with normal defect and abelian
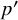 $p'$ inertial quotient
$p'$ inertial quotient
- Part of:
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 01 March 2023, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Grassmanniennes affines tordues sur les entiers
- Part of:
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 February 2023, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Duclos–Exner’s conjecture about waveguides in strong uniform magnetic fields
- Part of:
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 February 2023, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation