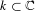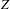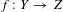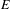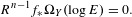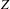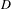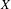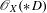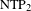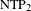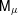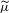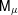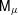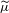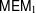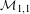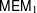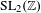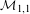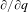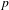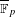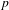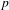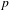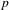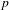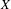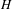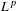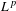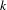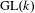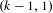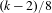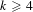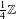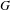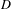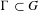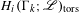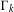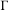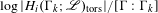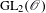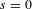980 results in Journal of the Institute of Mathematics of Jussieu
DISTINGUISHED MODELS OF INTERMEDIATE JACOBIANS
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 08 June 2018, pp. 891-918
- Print publication:
- May 2020
-
- Article
- Export citation
INTEGRAL AND ADELIC ASPECTS OF THE MUMFORD–TATE CONJECTURE
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 07 June 2018, pp. 869-890
- Print publication:
- May 2020
-
- Article
- Export citation
SYMMETRIC OPERADS IN ABSTRACT SYMMETRIC SPECTRA
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 25 May 2018, pp. 707-758
- Print publication:
- July 2019
-
- Article
- Export citation
LOCAL VANISHING AND HODGE FILTRATION FOR RATIONAL SINGULARITIES
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 17 May 2018, pp. 801-819
- Print publication:
- May 2020
-
- Article
- Export citation
A WEAK HILBERT SPACE THAT IS A TWISTED HILBERT SPACE
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 15 May 2018, pp. 855-867
- Print publication:
- May 2020
-
- Article
- Export citation
STABILIZERS,
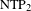 $\text{NTP}_{2}$ GROUPS WITH
$\text{NTP}_{2}$ GROUPS WITH  $\text{f}$-GENERICS, AND PRC FIELDS
$\text{f}$-GENERICS, AND PRC FIELDS
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 10 May 2018, pp. 821-853
- Print publication:
- May 2020
-
- Article
- Export citation
RANDOM SPARSE SAMPLING IN A GIBBS WEIGHTED TREE AND PHASE TRANSITIONS
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 09 May 2018, pp. 65-116
- Print publication:
- January 2020
-
- Article
- Export citation
UNIVERSAL MIXED ELLIPTIC MOTIVES
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 30 April 2018, pp. 663-766
- Print publication:
- May 2020
-
- Article
- Export citation
UNIVERSAL COVERS OF COMMUTATIVE FINITE MORLEY RANK GROUPS
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 26 April 2018, pp. 767-799
- Print publication:
- May 2020
-
- Article
- Export citation
JMJ volume 17 Issue 3 Cover and Back matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 23 April 2018, pp. b1-b5
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
JMJ volume 17 Issue 3 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 23 April 2018, pp. f1-f2
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
UNRAMIFIEDNESS OF GALOIS REPRESENTATIONS ATTACHED TO HILBERT MODULAR FORMS MOD
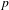 $p$ OF WEIGHT 1
$p$ OF WEIGHT 1
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 23 April 2018, pp. 281-306
- Print publication:
- March 2020
-
- Article
- Export citation
A BOUND FOR THE INDEX OF A QUADRATIC FORM AFTER SCALAR EXTENSION TO THE FUNCTION FIELD OF A QUADRIC
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 16 April 2018, pp. 421-450
- Print publication:
- March 2020
-
- Article
- Export citation
GENERAL HYPERPLANE SECTIONS OF THREEFOLDS IN POSITIVE CHARACTERISTIC
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 12 April 2018, pp. 647-661
- Print publication:
- March 2020
-
- Article
- Export citation
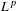 $L^{p}$ ESTIMATES FOR THE HOMOGENIZATION OF STOKES PROBLEM IN A PERFORATED DOMAIN
$L^{p}$ ESTIMATES FOR THE HOMOGENIZATION OF STOKES PROBLEM IN A PERFORATED DOMAIN
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 10 April 2018, pp. 231-258
- Print publication:
- January 2020
-
- Article
- Export citation
A COMPACTNESS THEOREM FOR SURFACES WITH BOUNDED INTEGRAL CURVATURE
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 10 April 2018, pp. 597-645
- Print publication:
- March 2020
-
- Article
- Export citation
EPSTEIN ZETA-FUNCTIONS, SUBCONVEXITY, AND THE PURITY CONJECTURE
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 02 April 2018, pp. 581-596
- Print publication:
- March 2020
-
- Article
- Export citation
PROJECTIVE STRUCTURES AND
 $\unicode[STIX]{x1D70C}$-CONNECTIONS
$\unicode[STIX]{x1D70C}$-CONNECTIONS
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 22 March 2018, pp. 571-579
- Print publication:
- March 2020
-
- Article
- Export citation
ON THE GROWTH OF TORSION IN THE COHOMOLOGY OF ARITHMETIC GROUPS
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 21 March 2018, pp. 537-569
- Print publication:
- March 2020
-
- Article
- Export citation
PERIODS OF DRINFELD MODULES AND LOCAL SHTUKAS WITH COMPLEX MULTIPLICATION
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 20 March 2018, pp. 175-208
- Print publication:
- January 2020
-
- Article
- Export citation