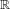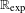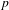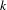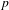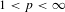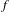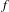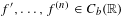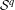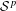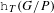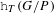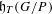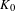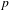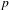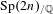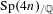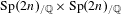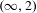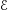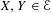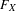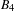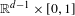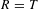980 results in Journal of the Institute of Mathematics of Jussieu
RAMSEY GROWTH IN SOME NIP STRUCTURES
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 19 February 2019, pp. 1-29
- Print publication:
- January 2021
-
- Article
- Export citation
ON THE
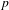 $p$-ADIC VARIATION OF HEEGNER POINTS
$p$-ADIC VARIATION OF HEEGNER POINTS
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 18 February 2019, pp. 2127-2164
- Print publication:
- November 2020
-
- Article
- Export citation
WEIERSTRASS PRYM EIGENFORMS IN GENUS FOUR
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 14 February 2019, pp. 2045-2085
- Print publication:
- November 2020
-
- Article
- Export citation
HIGHER ORDER DIFFERENTIABILITY OF OPERATOR FUNCTIONS IN SCHATTEN NORMS
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 13 February 2019, pp. 1993-2016
- Print publication:
- November 2020
-
- Article
- Export citation
PARABOLIC KAZHDAN–LUSZTIG BASIS, SCHUBERT CLASSES, AND EQUIVARIANT ORIENTED COHOMOLOGY
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 11 February 2019, pp. 1889-1929
- Print publication:
- November 2020
-
- Article
- Export citation
TOWARDS A NON-ARCHIMEDEAN ANALYTIC ANALOG OF THE BASS–QUILLEN CONJECTURE
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1931-1946
- Print publication:
- November 2020
-
- Article
- Export citation
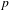 $p$-ADIC
$p$-ADIC  $L$-FUNCTIONS FOR ORDINARY FAMILIES ON SYMPLECTIC GROUPS
$L$-FUNCTIONS FOR ORDINARY FAMILIES ON SYMPLECTIC GROUPS
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 14 January 2019, pp. 1287-1347
- Print publication:
- July 2020
-
- Article
- Export citation
NON-HYPERBOLIC ERGODIC MEASURES AND HORSESHOES IN PARTIALLY HYPERBOLIC HOMOCLINIC CLASSES
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1765-1792
- Print publication:
- September 2020
-
- Article
- Export citation
ANALYTIC HYPOELLIPTICITY FOR SUMS OF SQUARES IN THE PRESENCE OF SYMPLECTIC NON TREVES STRATA
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1877-1888
- Print publication:
- November 2020
-
- Article
- Export citation
CATEGORICAL PROOF OF HOLOMORPHIC ATIYAH–BOTT FORMULA
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 20 December 2018, pp. 1739-1763
- Print publication:
- September 2020
-
- Article
- Export citation
LARGE-SCALE SUBLINEARLY LIPSCHITZ GEOMETRY OF HYPERBOLIC SPACES
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 1831-1876
- Print publication:
- November 2020
-
- Article
- Export citation
ON TYPICALITY OF TRANSLATION FLOWS WHICH ARE DISJOINT WITH THEIR INVERSE
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 11 December 2018, pp. 1677-1737
- Print publication:
- September 2020
-
- Article
- Export citation
JMJ volume 18 Issue 1 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 11 December 2018, pp. f1-f2
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
JMJ volume 18 Issue 1 Cover and Back matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 11 December 2018, pp. b1-b2
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
ANALOGUES OF CENTRALIZER SUBALGEBRAS FOR FIAT 2-CATEGORIES AND THEIR 2-REPRESENTATIONS
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 04 December 2018, pp. 1793-1829
- Print publication:
- November 2020
-
- Article
- Export citation
ZERO-LOCI OF BRAUER GROUP ELEMENTS ON SEMI-SIMPLE ALGEBRAIC GROUPS
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1467-1507
- Print publication:
- September 2020
-
- Article
- Export citation
WKB EXPANSIONS FOR HYPERBOLIC BOUNDARY VALUE PROBLEMS IN A STRIP: SELFINTERACTION MEETS STRONG WELL-POSEDNESS
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1629-1675
- Print publication:
- September 2020
-
- Article
- Export citation
SYMMETRIC POWER CONGRUENCE IDEALS AND SELMER GROUPS
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 14 November 2018, pp. 1521-1572
- Print publication:
- September 2020
-
- Article
- Export citation
SPECTRAL ANALYSIS OF MORSE–SMALE FLOWS I: CONSTRUCTION OF THE ANISOTROPIC SPACES
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 13 November 2018, pp. 1409-1465
- Print publication:
- September 2020
-
- Article
- Export citation
BEYOND ENDOSCOPY VIA THE TRACE FORMULA – IIITHE STANDARD REPRESENTATION
- Part of:
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 12 November 2018, pp. 1349-1387
- Print publication:
- July 2020
-
- Article
- Export citation