The discriminant of a trinomial of the form $x^{n}\pm \,x^{m}\pm \,1$ has the form $\pm n^{n}\pm (n-m)^{n-m}m^{m}$ if $n$ and $m$ are relatively prime. We investigate when these discriminants have nontrivial square factors. We explain various unlikely-seeming parametric families of square factors of these discriminant values: for example, when $n$ is congruent to 2 (mod 6) we have that $((n^{2}-n+1)/3)^{2}$ always divides $n^{n}-(n-1)^{n-1}$ . In addition, we discover many other square factors of these discriminants that do not fit into these parametric families. The set of primes whose squares can divide these sporadic values as $n$ varies seems to be independent of $m$ , and this set can be seen as a generalization of the Wieferich primes, those primes $p$ such that $2^{p}$ is congruent to 2 (mod $p^{2}$ ). We provide heuristics for the density of these sporadic primes and the density of squarefree values of these trinomial discriminants.

Researchers from across the social sciences have found consistent deviations from the predictions of the canonical model of self-interest in hundreds of experiments from around the world. This research, however, cannot determine whether the uniformity results from universal patterns of human behavior or from the limited cultural variation available among the university students used in virtually all prior experimental work. To address this, we undertook a cross-cultural study of behavior in ultimatum, public goods, and dictator games in a range of small-scale societies exhibiting a wide variety of economic and cultural conditions. We found, first, that the canonical model – based on self-interest – fails in all of the societies studied. Second, our data reveal substantially more behavioral variability across social groups than has been found in previous research. Third, group-level differences in economic organization and the structure of social interactions explain a substantial portion of the behavioral variation across societies: the higher the degree of market integration and the higher the payoffs to cooperation in everyday life, the greater the level of prosociality expressed in experimental games. Fourth, the available individual-level economic and demographic variables do not consistently explain game behavior, either within or across groups. Fifth, in many cases experimental play appears to reflect the common interactional patterns of everyday life.

We would like to thank the commentators for their generous comments, valuable insights and helpful suggestions. We begin this response by discussing the selfishness axiom and the importance of the preferences, beliefs, and constraints framework as a way of modeling some of the proximate influences on human behavior. Next, we broaden the discussion to ultimate-level (that is evolutionary) explanations, where we review and clarify gene-culture coevolutionary theory, and then tackle the possibility that evolutionary approaches that exclude culture might be sufficient to explain the data. Finally, we consider various methodological and epistemological concerns expressed by our commentators.

An explicit formula is derived for the logarithmic Mahler measure $m(P)$ of $P(x,\,y)\,=\,P(x)y-q(x)$ , where $p(x)$ and $q(x)$ are cyclotomic. This is used to find many examples of such polynomials for which $m(P)$ is rationally related to the Dedekind zeta value ${{\text{ }\!\!\zeta\!\!\text{ }}_{F}}(2)$ for certain quadratic and quartic fields.

If 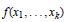$f({{x}_{1}},...,{{x}_{k}})$ is a polynomial with complex coefficients, the Mahler measure o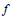f $f$ , 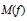$M(f)$ is defined to be the geometric mean of 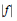$|f|$ over the $k$ -torus 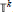${{\mathbb{T}}^{k}}$ . We construct a sequence of approximations 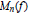${{M}_{n}}\,(f)$ which satisfy 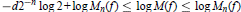$-d{{2}^{-n}}\,\log \,2\,+\,\log \,{{M}_{n}}(f)\,\le \,\log \,M(f)\,\le \,\log \,{{M}_{n}}(f)$ . We use these to prove that 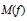$M(f)$ is a continuous function of the coefficients of 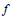$f$ for polynomials of fixed total degree 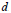$d$ . Since 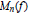${{M}_{n}}\,(f)$ can be computed in a finite number of arithmetic operations from the coefficients of 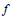$f$ this also demonstrates an effective (but impractical) method for computing 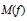$M(f)$ to arbitrary accuracy.

We are interested in how small a root of multiplicity k can be for a power series of the form f(z:=1+[sum ]∞n=1aiziwith coefficients ai in [−1, 1]. Let r(k) denote the size of the smallest root of multiplicity k possible for such a power series. We show that

formula here

We describe the form that the extremal power series must take and develop an algorithm that lets us compute the optimal root (which proves to be an algebraic number). The computations, for k[les ]27, suggest that the upper bound is close to optimal and that r(k)∼1−c/(k+1), where c=1.230….

Let f(x) be a monic polynomial of degree n with complex coefficients, which factors as f(x) = g(x)h(x), where g and h are monic. Let be the maximum of on the unit circle. We prove that , where β = M(P0) = 1 38135 …, where P0 is the polynomial P0(x, y) = 1 + x + y and δ = M(P1) = 1 79162…, where P1(x, y) = 1 + x + y - xy, and M denotes Mahler's measure. Both inequalities are asymptotically sharp as n → ∞.

The Mahler measure M (α) of an algebraic integer α is the product of the moduli of the conjugates of α which lie outside the unit circle. A number α is reciprocal if α- 1 is a conjugate of α. We give two constructions of reciprocal a for which M (α) is non-reciprocal producing examples of any degree n of the form 2h with h odd and h ≥ 3, or else of the form with s ≥ 2. We give explicit examples of degrees 10, 14 and 20.

The Mahler measure M(α) of an algebraic integer α is the product of the absolute value of the conjugates of α which lie outside the unit circle. The quantity log M(α) occurs in ergodic theory as the entropy of an endomorphism of the torus. Adler and Marcus showed that if β = M(α) then β is a Perron number which is a unit if α is a unit. They asked whether the Perron number β whose minimal polynomial is tm −t −1 is the measure of any algebraic integer. We show here that the answer is negative for all m > 3.

I would like to express my thanks to the Canadian Mathematical Society for inviting me to present this lecture. I would also like to express my appreciation to C.J. Smyth for numerous helpful conversations during his visit this year at the University of British Columbia.

This paper follows reasonably closely the outline of the lecture presented in Ottawa. More details are given here though and a number of proofs which would not be otherwise accessible have been added as Appendices. The attentive reader will soon realize the appropriateness of the title.