This paper establishes general theorems which contain both moduli of continuity and large incremental results for ${{l}^{\infty }}$ -valued Gaussian random fields indexed by a multidimensional parameter under explicit conditions.

We study strong asymptotic properties of two types of integral functionals of geometric stochastic processes. These integral functionals are of interest in financial modelling, yielding various option pricings, annuities, etc., by appropriate selection of the processes in their respective integrands. We show that under fairly general conditions on the latter processes the logs of the integral functionals themselves asymptotically behave like appropriate sup functionals of the processes in the exponents of their respective integrands. We illustrate the possible use and applications of these strong invariance theorems by listing and elaborating on several examples.

By using Chibisov-O'Reilly type theorems for uniform empirical and quantile processes based on stationary observations, we establish a weak approximation theory for empirical Lorenz curves and their inverses used in economics. In particular, we obtain weak approximations for empirical Lorenz curves and their inverses also under the assumptions of mixing dependence, often used structures of dependence for observations.

We study path properties of kernel generated two-time parameter, not necessarily stationary, Gaussian processes. We establish large deviation results for some increments of these processes and use these results to prove some of their moduli of continuity and other path properties.

We obtain weak and strong Gaussian approximations for logarithmic averages of indicators of normalized partial sums. The proofs are based on invariance principles for integrals of an Ornstein–Uhlenbeck process and on strong approximations of normalized partial sums by Orstein–Uhlenbeck processes.

Let be a sequence of independent Ornstein-Uhlenbeck processes with coefficients lk and ƛk,i.e., Xk(.)is a Gaussian process with EXk(t) =0 and

The process Y(.)was first studied by Dawson (1972) as the stationary solution of the infinite array of stochastic differential equations

where are independent Wiener processes (cf. also [6],[19],and [1]).

We prove strong approximations for partial sums indexed by a renewal process. The obtained results are optimal. The established probability inequalities are also used to get bounds for the rate of convergence of some limit theorems in queueing theory.

Let{N(x), x ≥ 0} be a Poisson process with intensity parameter λ > 0, and introduce

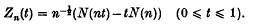
When looking for the changepoint in the Land's End data, Kendall and Kendall [7] proved for all 0 < ε1 < 1 − ε2 < 1 that

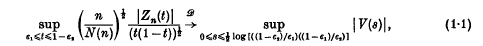
where {V(s), − ∞ < s < ∞} is an Ornstein–Uhlenbeck process with covariance function exp (−|t − s|). D. G. Kendall has posed the problem of replacing ε1 and ε2 by zero or by sequences εi(n) → 0 (n → ∞) (i = 1, 2), in (1·1). In this paper we study the latter problem and also its L2 version. The proofs will be based on the following weighted approximation of Zn.

Bachelier (1900), Einstein (1905) and Smoluchowski (1915) provided a theory of the peculiar erratic motion of small particles suspended in a liquid, first described in 1826 by the English botanist Brown. In a series of papers beginning in 1920 Wiener undertook a mathematical analysis of Brownian motion.

Let X1 …, Xn be mutually independent random variables with a common continuous distribution function F (t). Let Fn(t) be the corresponding empirical distribution function, that is

Fn(t) = (number of Xi ≤ t, 1 ≤ i ≤ n)/n.

Using a theorem of Manija [4], we proved among others the following statement in [1].

Let X1 X2, … , Xn be mutually independent random variables with a common continuous distribution function F(t). Let Fn(t) be the corresponding empirical distribution function, that is Fn(t) = (number of Xi ⩽ t, 1 ⩽ i ⩽ n)/n.

Let F(x) be the continuous distribution function of a random variable X and Fn(x) be the empirical distribution function determined by a random sample X1, …, Xn taken on X. Using the method of Birnbaum and Tingey [1] we are going to derive the exact distributions of the random variables

and and where the indicated sup' s are taken over all x' s such that -∞ < x < xb and xa ≤ x < + ∞ with F(xb) = b, F(xa) = a in the first two cases and over all x' s so that Fn(x) ≤ b and a ≤ Fn(x) in the last two cases.