 $\mathfrak{M}_H(G)$-property
$\mathfrak{M}_H(G)$-property
 $\tau $-component in the Iwasawa main conjecture
$\tau $-component in the Iwasawa main conjecture
 ${\mathbb{Z}}_p$-towers
${\mathbb{Z}}_p$-towers
 $\mu$-invariant of two-variable
$\mu$-invariant of two-variable  $2$-adic
$2$-adic  $\boldsymbol{L}$-functions
$\boldsymbol{L}$-functions
 $\mu $-invariants of supersingular elliptic curves
$\mu $-invariants of supersingular elliptic curves
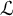 $\mathcal {L}$-invariants and Fontaine–Mazur
$\mathcal {L}$-invariants and Fontaine–Mazur 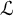 $\mathcal {L}$-invariants
$\mathcal {L}$-invariants
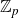 $\mathbb{Z}_{p}$-extensions
$\mathbb{Z}_{p}$-extensions
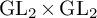 $\mathrm {GL}_2\times \mathrm {GL}_2$
$\mathrm {GL}_2\times \mathrm {GL}_2$
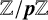 ${\mathbb {Z}}/\boldsymbol{p}{\mathbb {Z}}$-EXTENSIONS
${\mathbb {Z}}/\boldsymbol{p}{\mathbb {Z}}$-EXTENSIONS