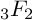 $_3F_2$(1)-SERIES
$_3F_2$(1)-SERIES
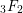 $_{3}F_{2}$
$_{3}F_{2}$
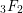 $_{3}F_{2}$
$_{3}F_{2}$
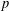 $p$ -ADIC GAMMA FUNCTIONS
$p$ -ADIC GAMMA FUNCTIONS
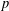 $p$ -ADIC HYPERGEOMETRIC FUNCTIONS
$p$ -ADIC HYPERGEOMETRIC FUNCTIONS