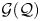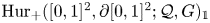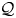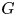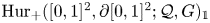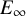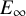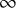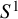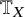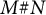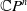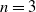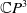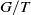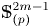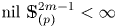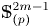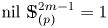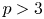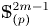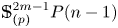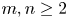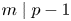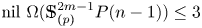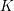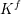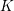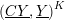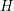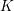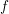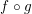Refine search
Actions for selected content:
22 results
Loop space decompositions of moment-angle complexes associated to two-dimensional simplicial complexes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-23
-
- Article
- Export citation
SU(2)-bundles over highly connected 8-manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 February 2025, pp. 1-30
-
- Article
- Export citation
Graphing, homotopy groups of spheres, and spaces of long links and knots
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 February 2025, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EPIMORPHISMS AND ACYCLIC TYPES IN UNIVALENT FOUNDATIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 February 2025, pp. 1-36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deloopings of Hurwitz spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1651-1714
- Print publication:
- July 2024
-
- Article
- Export citation
Adams’ cobar construction as a monoidal
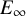 $E_{\infty }$-coalgebra model of the based loop space
$E_{\infty }$-coalgebra model of the based loop space
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 May 2024, e62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cogroupoid structures on the circle and the Hodge degeneration
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 January 2024, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moore’s conjecture for connected sums
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 04 December 2023, pp. 516-531
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reflexive homology
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1378-1405
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The rational homotopy type of homotopy fibrations over connected sums
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 03 April 2023, pp. 133-142
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Homotopy commutativity in Hermitian symmetric spaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 18 April 2022, pp. 746-752
- Print publication:
- September 2022
-
- Article
- Export citation
Massey products in the homology of the loop space of a p-completed classifying space: finite groups with cyclic Sylow p-subgroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 30 September 2021, pp. 908-915
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Homotopy nilpotency of localized spheres and projective spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 501-512
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RATIONAL LOCAL SYSTEMS AND CONNECTED FINITE LOOP SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 14 January 2021, pp. 136-164
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
The fibre of the degree 3 map, Anick spaces and the double suspension
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 21 July 2020, pp. 830-843
-
- Article
- Export citation
Higher homotopy associativity in the Harris decomposition of Lie groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 11 September 2019, pp. 2982-3000
- Print publication:
- December 2020
-
- Article
- Export citation
Koszul A∞-algebras and free loop space homology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 37-65
-
- Article
- Export citation
The homotopy theory of polyhedral products associated with flag complexes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 23 November 2018, pp. 206-228
- Print publication:
- January 2019
-
- Article
- Export citation
Module structure on Lie powers and natural coalgebra-split sub-Hopf algebras of tensor algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 04 April 2011, pp. 467-504
-
- Article
-
- You have access
- Export citation
The Vanishing problem of the string class with degree 3
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 1 / August 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-142
- Print publication:
- August 1998
-
- Article
-
- You have access
- Export citation