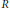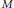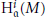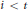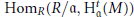Refine search
Actions for selected content:
26 results
Ideals and their Fitting ideals
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 30 July 2025, pp. 609-621
- Print publication:
- November 2025
-
- Article
- Export citation
Locally compact modules over abelian groups and compactly generated metabelian groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1250-1283
- Print publication:
- June 2025
-
- Article
- Export citation
LOCAL COHOMOLOGY UNDER SMALL PERTURBATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 183-200
- Print publication:
- June 2025
-
- Article
- Export citation
Classification of multiplication modules over multiplication rings with finitely many minimal primes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 03 October 2024, pp. 67-71
- Print publication:
- January 2025
-
- Article
- Export citation
ISOMORPHISM OF RELATIVE HOLOMORPHS AND MATRIX SIMILARITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 23 September 2024, pp. 298-313
- Print publication:
- April 2025
-
- Article
- Export citation
Ulrich modules and weakly lim Ulrich sequences do not always exist
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 10 August 2023, e71
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NEW ALGORITHM FOR DECOMPOSING MODULAR TENSOR PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 11 January 2021, pp. 94-107
- Print publication:
- August 2021
-
- Article
- Export citation
A Module-theoretic Characterization of Algebraic Hypersurfaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 1 / 01 March 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 166-173
- Print publication:
- 01 March 2018
-
- Article
-
- You have access
- Export citation
On the Universal SL2-Representation Rings of Free Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 973-1001
-
- Article
- Export citation
Irreducible decomposition of binomial ideals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 1319-1332
- Print publication:
- June 2016
-
- Article
- Export citation
Quasi-copure Submodules
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 1 / 01 March 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 197-203
- Print publication:
- 01 March 2016
-
- Article
-
- You have access
- Export citation
On the Theorem of the Primitive Element with Applications to the Representation Theory of Associative and Lie Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 4 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 735-748
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
Corrigendum: Filtering free resolutions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 9 / September 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 1482-1484
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
Filtering free resolutions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 5 / May 2013
- Published online by Cambridge University Press:
- 18 March 2013, pp. 754-772
- Print publication:
- May 2013
-
- Article
- Export citation
On Modules Whose Proper Homomorphic Images Are of Smaller Cardinality
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 2 / 01 June 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 378-389
- Print publication:
- 01 June 2012
-
- Article
-
- You have access
- Export citation
Cohen-Macaulay binomial edge ideals
-
- Journal:
- Nagoya Mathematical Journal / Volume 204 / December 2011
- Published online by Cambridge University Press:
- 11 January 2016, pp. 57-68
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
FINITELY GENERATED GRADED MULTIPLICATION MODULES
-
- Journal:
- Glasgow Mathematical Journal / Volume 53 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 01 August 2011, pp. 693-705
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
φ-PRIME SUBMODULES
-
- Journal:
- Glasgow Mathematical Journal / Volume 52 / Issue 2 / May 2010
- Published online by Cambridge University Press:
- 25 November 2009, pp. 253-259
- Print publication:
- May 2010
-
- Article
-
- You have access
- Export citation
STRONGLY IRREDUCIBLE IDEALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 145-154
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
Artinian Local Cohomology Modules
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 4 / 01 December 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 598-602
- Print publication:
- 01 December 2007
-
- Article
-
- You have access
- Export citation

















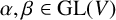
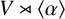
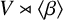
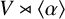

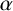

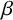

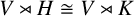
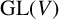
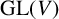
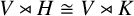
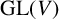
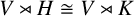
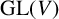
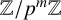
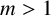
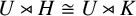
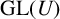
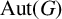
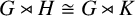
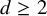
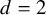
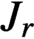

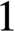
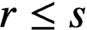



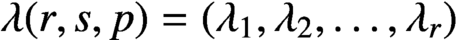
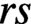

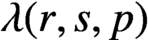
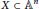

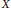
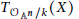
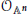

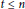

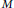
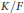
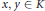

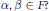

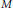

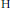
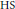
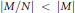
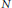
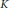
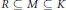

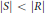
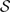
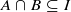 implies that either
implies that either 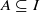 or
or 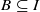 . In this paper we study strongly irreducible ideals in different rings. The relations between strongly irreducible ideals of a ring and strongly irreducible ideals of localizations of the ring are also studied. Furthermore, a topology similar to the Zariski topology related to strongly irreducible ideals is introduced. This topology has the Zariski topology defined by prime ideals as one of its subspace topologies.
. In this paper we study strongly irreducible ideals in different rings. The relations between strongly irreducible ideals of a ring and strongly irreducible ideals of localizations of the ring are also studied. Furthermore, a topology similar to the Zariski topology related to strongly irreducible ideals is introduced. This topology has the Zariski topology defined by prime ideals as one of its subspace topologies.