Let $\mathbf {G}$ be a connected reductive algebraic group over an algebraically closed field $\Bbbk $ and ${\mathbf B}$ be a Borel subgroup of ${\mathbf G}$. In this paper, we completely determine the composition factors of the permutation module $\mathbb {F}[{\mathbf G}/{\mathbf B}]$ for any field $\mathbb {F}$.

Nilpotency concepts for skew braces are among the main tools with which we are nowadays classifying certain special solutions of the Yang–Baxter equation, a consistency equation that plays a relevant role in quantum statistical mechanics and in many areas of mathematics. In this context, two relevant questions have been raised in F. Cedó, A. Smoktunowicz and L. Vendramin (Skew left braces of nilpotent type. Proc. Lond. Math. Soc. (3) 118 (2019), 1367–1392) (see questions 2.34 and 2.35) concerning right- and central nilpotency. The aim of this short note is to give a negative answer to both questions: thus, we show that a finite strong-nil brace B need not be right-nilpotent. On a positive note, we show that there is one (and only one, by our examples) special case of the previous questions that actually holds. In fact, we show that if B is a skew brace of nilpotent type and $b\ \ast \ b=0$ for all $b\in B$, then B is centrally nilpotent.

Let G be a torsion-free, finitely generated, nilpotent and metabelian group. In this work, we show that G embeds into the group of orientation-preserving $C^{1+\alpha }$-diffeomorphisms of the compact interval for all $\alpha < 1/k$, where k is the torsion-free rank of $G/A$ and A is a maximal abelian subgroup. We show that, in many situations, the corresponding $1/k$ is critical in the sense that there is no embedding of G with higher regularity. A particularly nice family where this happens is the family of $(2n+1)$-dimensional Heisenberg groups, for which we can show that the critical regularity is equal to $1+1/n$.

A well-known theorem of Philip Hall states that if a group G has a nilpotent normal subgroup N such that $G/N'$ is nilpotent, then G itself is nilpotent. We say that a group class 𝔛 is a Hall class if it contains every group G admitting a nilpotent normal subgroup N such that $G/N'$ belongs to 𝔛. Hall classes have been considered by several authors, such as Plotkin [‘Some properties of automorphisms of nilpotent groups’, Soviet Math. Dokl. 2 (1961), 471–474] and Robinson [‘A property of the lower central series of a group’, Math. Z. 107 (1968), 225–231]. A further detailed study of Hall classes is performed by us in another paper [‘Hall classes of groups’, to appear] and we also investigate the behaviour of the class of finite-by-𝔜 groups for a given Hall class 𝔜 [‘Hall classes in linear groups’, to appear]. The aim of this paper is to prove that for most natural choices of the Hall class 𝔜, also the classes $(\mathbf{L}\mathfrak{F})\mathfrak{Y}$ and 𝔅𝔜 are Hall classes, where L𝔉 is the class of locally finite groups and 𝔅 is the class of locally finite groups of finite exponent.

We calculate asymptotic estimates for the conjugacy growth function of finitely generated class 2 nilpotent groups whose derived subgroups are infinite cyclic, including the so-called higher Heisenberg groups. We prove that these asymptotics are stable when passing to commensurable groups, by understanding their twisted conjugacy growth. We also use these estimates to prove that, in certain cases, the conjugacy growth series cannot be a holonomic function.

Let $M(A,n)$ be the Moore space of type $(A,n)$ for an Abelian group A and $n\ge 2$. We show that the loop space $\Omega (M(A,n))$ is homotopy nilpotent if and only if A is a subgroup of the additive group $\mathbb {Q}$ of the field of rationals. Homotopy nilpotency of loop spaces $\Omega (M(A,1))$ is discussed as well.

For a finite group $G$, define $l(G)=(\prod _{g\in G}o(g))^{1/|G|}/|G|$, where $o(g)$ denotes the order of $g\in G$. We prove that if $l(G)>l(A_{5}),l(G)>l(A_{4}),l(G)>l(S_{3}),l(G)>l(Q_{8})$ or $l(G)>l(C_{2}\times C_{2})$, then $G$ is solvable, supersolvable, nilpotent, abelian or cyclic, respectively.

The class of all monolithic (that is, subdirectly irreducible) groups belonging to a variety generated by a finite nilpotent group can be axiomatised by a finite set of elementary sentences.

The subgroup commutativity degree of a group 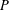$G$ is the probability that two subgroups of $G$ commute, or equivalently that the product of two subgroups is again a subgroup. For the dihedral, quasi-dihedral and generalised quaternion groups (all of 2-power cardinality), the subgroup commutativity degree tends to 0 as the size of the group tends to infinity. This also holds for the family of projective special linear groups over fields of even characteristic and for the family of the simple Suzuki groups. In this short note, we show that the family of finite $P$-groups also has this property.

We define a pseudometric on the set of all unbounded subsets of a metric space. The Kolmogorov quotient of this pseudometric space is a complete metric space. The definition of the pseudometric is guided by the principle that two unbounded subsets have distance 0 whenever they stay sublinearly close. Based on this pseudometric we introduce and study a general concept of boundaries of metric spaces. Such a boundary is the closure of a subset in the Kolmogorov quotient determined by an arbitrarily chosen family of unbounded subsets. Our interest lies in those boundaries which we get by choosing unbounded cyclic sub(semi)groups of a finitely generated group (or more general of a compactly generated, locally compact Hausdorff group). We show that these boundaries are quasi-isometric invariants and determine them in the case of nilpotent groups as a disjoint union of certain spheres (or projective spaces). In addition we apply this concept to vertex-transitive graphs with polynomial growth and to random walks on nilpotent groups.

We prove that if $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}S$ is a finite subset of an ordered group that generates a nonabelian ordered group, then $|S^2|\geq 3|S|-2$. This generalizes a classical result from the theory of set addition.

We prove some theorems on locally graded groups and nilpotent-by-Chernikov groups.

In this article the following are proved: 1. Let $G$ be an infinite $p$-group of cardinality either ${\bf {\mathbb N}_{0}}$ or greater than $2^{\bf {\mathbb N}_{0}}$. If $G$ is center-by-finite and non-$\skew5\check{C}$ernikov, then it is non-co-Hopfian; that is, $G$ is isomorphic to a proper subgroup of itself. 2. Let $G$ be a nilpotent $p$-group of class $2$ with $G/G'$ a non-$\skew5\check{C}$ernikov group of cardinality ${\bf {\mathbb N}_{0}}$ or greater than $2^{{\bf {\mathbb N}_{0}}}$. If $G'$ is of order $p$, then $G$ is non-co-Hopfian.

Let $G$ be a finitely generated, infinite group, let $p\,>\,1$ , and let ${{L}^{p}}\left( G \right)$ denote the Banach space $\left\{ \sum{_{x\in G}{{a}_{x}}x}|\sum{_{x\in G}|{{a}_{x}}{{|}^{p}}<\infty } \right\}$ . In this paper we will study the first cohomology gro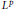up of $G$ with coefficients in ${{L}^{p}}\left( G \right)$ , and the first reduced ${{L}^{p}}$ -cohomology space of $G$ . Most of our results will be for a class of groups that contains all finitely generated, infinite nilpotent groups.

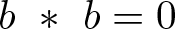
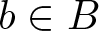
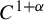
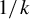
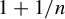
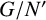
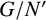
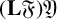
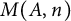
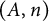
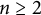
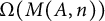
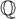
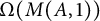
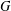
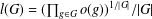
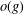
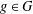
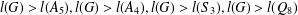
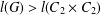
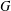
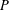
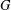
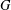
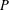
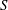
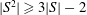
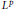
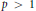
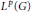
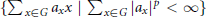
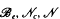Let and 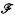denote respectively the variety of groups of exponent dividing 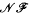e, the variety of nilpotent groups of class at most c, the class of nilpotent groups and the class of finite groups. It follows from a result due to Kargapolov and Čurkin and independently to Groves that in a variety not containing all metabelian groups, each polycyclic group G belongs to . We show that 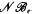G is in fact in , where c is an integer depending only on the variety. On the other hand, it is not always possible to find an integer e (depending only on the variety) such that G belongs to but we characterize the varieties in which that is possible. In this case, there exists a function 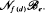f such that, if G is d-generated, then G ∈ So, when 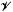e = 1, we obtain an extension of Zel'manov's result about the restricted Burnside problem (as one might expect, this result is used in our proof). Finally, we show that the class of locally nilpotent groups of a variety forms a variety if and only if 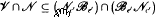for some integers c′, e′.

We prove that generalized free products of finitely generated free-byfinite or nilpotent-by-finite groups amalgamating a cyclic subgroup areconjugacy separable. Applying this result we prove a generalization of a conjecture of Fine and Rosenberger [7] that groups of F-type are conjugacy separable.

We show that, even under very favourable hypotheses, a polygonal product of finitely generated torsion free nilpotent groups amalgamating infinite cyclic subgroups is, in general, not residually finite, thus answering negatively a question of C. Y. Tang. A second example shows similar kinds of limitations apply even when the factors of the product are free abelian groups.

In this paper we show that any system of equations over a free nilpotent group of class c is either unitary or miliary. In fact, such a system either has a most general solution (akin to the most general solution of a system of linear dipohantine equations), or every solution has a proper generalization. In principle we provide an algorithm for determining whether or not a most general solution exists, and exhibiting it if it does.

In general polygonal products of finitely generated torsion-free nilpotent groups amalgamating cyclic subgroups need not be residually finite. In this paper we prove that polygonal products of finitely generated torsion-free nilpotent groups amalgamating maximal cyclic subgroups such that the amalgamated cycles generate an isolated subgroup in the vertex group containing them, are residually finite. We also prove that, for finitely generated torsion-free nilpotent groups, if the subgroups generated by the amalgamated cycles have the same nilpotency classes as their respective vertex groups, then their polygonal product is residually finite.

Let Mn, c denote the free n-generator metabelian nilpotent group of class c. For m ≤ n – 2, every primitive system of m elements of Mn, c can be lifted to a primitive system of m elements of the absolutely free group Fn of rank n. The restriction on m cannot be improved.