In this study, we consider the nonclassical diffusion equations with time-dependent memory kernels 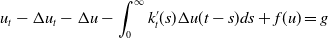 \begin{equation*} u_{t} - \Delta u_t - \Delta u - \int_0^\infty k^{\prime}_{t}(s) \Delta u(t-s) ds + f( u) = g \end{equation*}
\begin{equation*} u_{t} - \Delta u_t - \Delta u - \int_0^\infty k^{\prime}_{t}(s) \Delta u(t-s) ds + f( u) = g \end{equation*}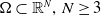 $\Omega \subset \mathbb{R}^N,\, N\geq 3$. Firstly, we study the existence and uniqueness of weak solutions and then, we investigate the existence of the time-dependent global attractors
$\Omega \subset \mathbb{R}^N,\, N\geq 3$. Firstly, we study the existence and uniqueness of weak solutions and then, we investigate the existence of the time-dependent global attractors 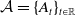 $\mathcal{A}=\{A_t\}_{t\in\mathbb{R}}$ in
$\mathcal{A}=\{A_t\}_{t\in\mathbb{R}}$ in 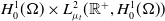 $H_0^1(\Omega)\times L^2_{\mu_t}(\mathbb{R}^+,H_0^1(\Omega))$. Finally, we prove that the asymptotic dynamics of our problem, when
$H_0^1(\Omega)\times L^2_{\mu_t}(\mathbb{R}^+,H_0^1(\Omega))$. Finally, we prove that the asymptotic dynamics of our problem, when 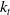 $k_t$ approaches a multiple
$k_t$ approaches a multiple 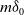 $m\delta_0$ of the Dirac mass at zero as
$m\delta_0$ of the Dirac mass at zero as 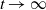 $t\to \infty$, is close to the one of its formal limit
$t\to \infty$, is close to the one of its formal limit 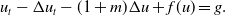 \begin{equation*}u_{t} - \Delta u_{t} - (1+m)\Delta u + f( u) = g. \end{equation*}
\begin{equation*}u_{t} - \Delta u_{t} - (1+m)\Delta u + f( u) = g. \end{equation*}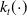 $k_t(\!\cdot\!)$ depends on time, which allows for instance to describe the dynamics of aging materials.
$k_t(\!\cdot\!)$ depends on time, which allows for instance to describe the dynamics of aging materials.