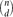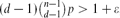Refine search
Actions for selected content:
48285 results in Computer Science
6 - Visualization and debugging
- from Part II - Application development
-
- Book:
- Fundamentals of Stream Processing
- Published online:
- 05 March 2014
- Print publication:
- 13 February 2014, pp 178-200
-
- Chapter
- Export citation
Part IV - Application design and analytics
-
- Book:
- Fundamentals of Stream Processing
- Published online:
- 05 March 2014
- Print publication:
- 13 February 2014, pp 273-274
-
- Chapter
- Export citation
Local Limit Theorems for the Giant Component of Random Hypergraphs†
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 3 / May 2014
- Published online by Cambridge University Press:
- 13 February 2014, pp. 331-366
-
- Article
- Export citation
1 - What brought us here?
- from Part 1 - Fundamentals
-
- Book:
- Fundamentals of Stream Processing
- Published online:
- 05 March 2014
- Print publication:
- 13 February 2014, pp 3-32
-
- Chapter
- Export citation
Contents
-
- Book:
- Fundamentals of Stream Processing
- Published online:
- 05 March 2014
- Print publication:
- 13 February 2014, pp vii-xii
-
- Chapter
- Export citation
Keywords and identifiers index
-
- Book:
- Fundamentals of Stream Processing
- Published online:
- 05 March 2014
- Print publication:
- 13 February 2014, pp 500-503
-
- Chapter
- Export citation
Part II - Application development
-
- Book:
- Fundamentals of Stream Processing
- Published online:
- 05 March 2014
- Print publication:
- 13 February 2014, pp 75-76
-
- Chapter
- Export citation
13 - Conclusion
- from Part VI - Closing notes
-
- Book:
- Fundamentals of Stream Processing
- Published online:
- 05 March 2014
- Print publication:
- 13 February 2014, pp 487-499
-
- Chapter
- Export citation
Acknowledgements
-
- Book:
- Fundamentals of Stream Processing
- Published online:
- 05 March 2014
- Print publication:
- 13 February 2014, pp xxi-xxi
-
- Chapter
- Export citation
Part 1 - Fundamentals
-
- Book:
- Fundamentals of Stream Processing
- Published online:
- 05 March 2014
- Print publication:
- 13 February 2014, pp 1-2
-
- Chapter
- Export citation
Preface
-
- Book:
- Fundamentals of Stream Processing
- Published online:
- 05 March 2014
- Print publication:
- 13 February 2014, pp xiii-xviii
-
- Chapter
- Export citation
8 - InfoSphere Streams architecture
- from Part III - System architecture
-
- Book:
- Fundamentals of Stream Processing
- Published online:
- 05 March 2014
- Print publication:
- 13 February 2014, pp 218-272
-
- Chapter
- Export citation
NLE volume 20 issue 2 Cover and Back matter
-
- Journal:
- Natural Language Engineering / Volume 20 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 11 February 2014, pp. b1-b4
-
- Article
-
- You have access
- Export citation
NLE volume 20 issue 2 Cover and Front matter
-
- Journal:
- Natural Language Engineering / Volume 20 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 11 February 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
SOME REMARKS ON DISTRIBUTED SENSING WITH COSTS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 28 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 11 February 2014, pp. 271-277
-
- Article
- Export citation
Abstract interpretation of temporal concurrent constraint programs
-
- Journal:
- Theory and Practice of Logic Programming / Volume 15 / Issue 3 / May 2015
- Published online by Cambridge University Press:
- 10 February 2014, pp. 312-357
-
- Article
- Export citation
2 - Perfect Graphs and Graphical Modeling
- from Part 1 - Graphical Structure
-
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 39-68
-
- Chapter
- Export citation