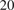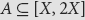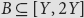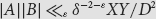Refine search
Actions for selected content:
48585 results in Computer Science
Logic and learning in network cascades
-
- Journal:
- Network Science / Volume 9 / Issue S1 / October 2021
- Published online by Cambridge University Press:
- 14 April 2021, pp. S157-S174
-
- Article
-
- You have access
- Open access
- Export citation

Nigeria's Digital Diaspora
- Citizen Media, Democracy, and Participation
-
- Published by:
- Boydell & Brewer
- Published online:
- 13 April 2021
- Print publication:
- 15 January 2020
Ramsey-type numbers involving graphs and hypergraphs with large girth
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 12 April 2021, pp. 722-740
-
- Article
- Export citation
Feature extraction and artificial neural networks for the on-the-fly classification of high-dimensional thermochemical spaces in adaptive-chemistry simulations
-
- Journal:
- Data-Centric Engineering / Volume 2 / 2021
- Published online by Cambridge University Press:
- 12 April 2021, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polynomial-time approximation algorithms for the antiferromagnetic Ising model on line graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 12 April 2021, pp. 905-921
-
- Article
- Export citation

Privacy in the Age of Neuroscience
- Reimagining Law, State and Market
-
- Published online:
- 09 April 2021
- Print publication:
- 15 April 2021

Exploring Malicious Hacker Communities
- Toward Proactive Cyber-Defense
-
- Published online:
- 09 April 2021
- Print publication:
- 29 April 2021
Acknowledgements
-
- Book:
- Technology Law
- Published online:
- 21 April 2021
- Print publication:
- 08 April 2021, pp xix-xx
-
- Chapter
- Export citation
12 - When All Is Quiet
-
- Book:
- Hey Cyba
- Published online:
- 26 March 2021
- Print publication:
- 08 April 2021, pp 183-194
-
- Chapter
- Export citation
Table of cases
-
- Book:
- Technology Law
- Published online:
- 21 April 2021
- Print publication:
- 08 April 2021, pp x-xiii
-
- Chapter
- Export citation
6 - Uncertainty Relations and Sparse Signal Recovery
-
-
- Book:
- Information-Theoretic Methods in Data Science
- Published online:
- 22 March 2021
- Print publication:
- 08 April 2021, pp 163-196
-
- Chapter
- Export citation
3 - Compressed Sensing via Compression Codes
-
-
- Book:
- Information-Theoretic Methods in Data Science
- Published online:
- 22 March 2021
- Print publication:
- 08 April 2021, pp 72-103
-
- Chapter
- Export citation
Facilitating design: examining the effects of facilitator’s neutrality on trust and potency in an exploratory experimental study
-
- Journal:
- Design Science / Volume 7 / 2021
- Published online by Cambridge University Press:
- 08 April 2021, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
8 - Social media and communications
-
- Book:
- Technology Law
- Published online:
- 21 April 2021
- Print publication:
- 08 April 2021, pp 162-183
-
- Chapter
- Export citation
Index
-
- Book:
- Technology Law
- Published online:
- 21 April 2021
- Print publication:
- 08 April 2021, pp 227-238
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Hey Cyba
- Published online:
- 26 March 2021
- Print publication:
- 08 April 2021, pp i-iv
-
- Chapter
- Export citation
Physical prototyping rationale in design student projects: an analysis based on the concept of purposeful prototyping
-
- Journal:
- Design Science / Volume 7 / 2021
- Published online by Cambridge University Press:
- 08 April 2021, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
13 - Statistical Problems with Planted Structures: Information-Theoretical and Computational Limits
-
-
- Book:
- Information-Theoretic Methods in Data Science
- Published online:
- 22 March 2021
- Print publication:
- 08 April 2021, pp 383-424
-
- Chapter
- Export citation
13 - Future Upgrades and Beyond
-
- Book:
- Hey Cyba
- Published online:
- 26 March 2021
- Print publication:
- 08 April 2021, pp 195-210
-
- Chapter
- Export citation
Extremal problems for GCDs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 08 April 2021, pp. 922-929
-
- Article
-
- You have access
- Open access
- Export citation