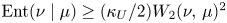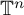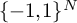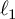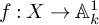Refine search
Actions for selected content:
25823 results in Abstract analysis
Transportation on spheres via an entropy formula
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 1467-1478
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on monotonicity and Bochner formulas in Carnot groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 1543-1563
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
VARIANTS OF A MULTIPLIER THEOREM OF KISLYAKOV
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 01 September 2022, pp. 347-377
- Print publication:
- January 2024
-
- Article
- Export citation
JMJ volume 21 issue 5 Cover and Back matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 02 September 2022, pp. b1-b2
- Print publication:
- September 2022
-
- Article
-
- You have access
- Export citation
JMJ volume 21 issue 5 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 02 September 2022, pp. f1-f2
- Print publication:
- September 2022
-
- Article
-
- You have access
- Export citation
A DERIVED LAGRANGIAN FIBRATION ON THE DERIVED CRITICAL LOCUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 31 August 2022, pp. 311-345
- Print publication:
- January 2024
-
- Article
- Export citation
Truncated versions of three identities of Euler and Gauss
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 30 August 2022, pp. 775-798
-
- Article
- Export citation
Part I - Elements of Probability Theory
-
- Book:
- Principles of Statistical Analysis
- Published online:
- 22 July 2022
- Print publication:
- 25 August 2022, pp 1-2
-
- Chapter
- Export citation
21 - Regression Analysis
- from Part III - Elements of Statistical Inference
-
- Book:
- Principles of Statistical Analysis
- Published online:
- 22 July 2022
- Print publication:
- 25 August 2022, pp 329-355
-
- Chapter
- Export citation
3 - Distributions on the Real Line
- from Part I - Elements of Probability Theory
-
- Book:
- Principles of Statistical Analysis
- Published online:
- 22 July 2022
- Print publication:
- 25 August 2022, pp 34-40
-
- Chapter
- Export citation
Dedication
-
- Book:
- Principles of Statistical Analysis
- Published online:
- 22 July 2022
- Print publication:
- 25 August 2022, pp vii-vii
-
- Chapter
- Export citation
6 - Multivariate Distributions
- from Part I - Elements of Probability Theory
-
- Book:
- Principles of Statistical Analysis
- Published online:
- 22 July 2022
- Print publication:
- 25 August 2022, pp 68-77
-
- Chapter
- Export citation
17 - Multiple Numerical Samples
- from Part III - Elements of Statistical Inference
-
- Book:
- Principles of Statistical Analysis
- Published online:
- 22 July 2022
- Print publication:
- 25 August 2022, pp 271-288
-
- Chapter
- Export citation
10 - Sampling and Simulation
- from Part II - Practical Considerations
-
- Book:
- Principles of Statistical Analysis
- Published online:
- 22 July 2022
- Print publication:
- 25 August 2022, pp 127-137
-
- Chapter
- Export citation
7 - Expectation and Concentration
- from Part I - Elements of Probability Theory
-
- Book:
- Principles of Statistical Analysis
- Published online:
- 22 July 2022
- Print publication:
- 25 August 2022, pp 78-99
-
- Chapter
- Export citation
Part II - Practical Considerations
-
- Book:
- Principles of Statistical Analysis
- Published online:
- 22 July 2022
- Print publication:
- 25 August 2022, pp 125-126
-
- Chapter
- Export citation
Contents
-
- Book:
- Principles of Statistical Analysis
- Published online:
- 22 July 2022
- Print publication:
- 25 August 2022, pp ix-xiii
-
- Chapter
- Export citation
8 - Convergence of Random Variables
- from Part I - Elements of Probability Theory
-
- Book:
- Principles of Statistical Analysis
- Published online:
- 22 July 2022
- Print publication:
- 25 August 2022, pp 100-112
-
- Chapter
- Export citation
9 - Stochastic Processes
- from Part I - Elements of Probability Theory
-
- Book:
- Principles of Statistical Analysis
- Published online:
- 22 July 2022
- Print publication:
- 25 August 2022, pp 113-124
-
- Chapter
- Export citation
4 - Discrete Distributions
- from Part I - Elements of Probability Theory
-
- Book:
- Principles of Statistical Analysis
- Published online:
- 22 July 2022
- Print publication:
- 25 August 2022, pp 41-53
-
- Chapter
- Export citation