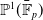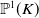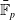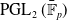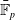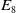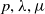Refine search
Actions for selected content:
25839 results in Abstract analysis
Notation Index
-
- Book:
- Hardy Martingales
- Published online:
- 30 June 2022
- Print publication:
- 14 July 2022, pp 223-497
-
- Chapter
- Export citation
2 - Hardy Martingales
-
- Book:
- Hardy Martingales
- Published online:
- 30 June 2022
- Print publication:
- 14 July 2022, pp 87-135
-
- Chapter
- Export citation
6 - Operators on Lp (L1)
-
- Book:
- Hardy Martingales
- Published online:
- 30 June 2022
- Print publication:
- 14 July 2022, pp 391-426
-
- Chapter
- Export citation
Subject Index
-
- Book:
- Hardy Martingales
- Published online:
- 30 June 2022
- Print publication:
- 14 July 2022, pp 498-500
-
- Chapter
- Export citation
Dedication
-
- Book:
- Hardy Martingales
- Published online:
- 30 June 2022
- Print publication:
- 14 July 2022, pp v-vi
-
- Chapter
- Export citation
5 - Isomorphic Invariants
-
- Book:
- Hardy Martingales
- Published online:
- 30 June 2022
- Print publication:
- 14 July 2022, pp 274-390
-
- Chapter
- Export citation
7 - Formative Examples
-
- Book:
- Hardy Martingales
- Published online:
- 30 June 2022
- Print publication:
- 14 July 2022, pp 427-482
-
- Chapter
- Export citation
1 - Stochastic Holomorphy
-
- Book:
- Hardy Martingales
- Published online:
- 30 June 2022
- Print publication:
- 14 July 2022, pp 1-86
-
- Chapter
- Export citation
Automorphism groups of endomorphisms of
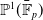 $\mathbb{P}^1 (\bar{\mathbb{F}}_p)$
$\mathbb{P}^1 (\bar{\mathbb{F}}_p)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 13 July 2022, pp. 222-255
-
- Article
- Export citation
Resilient tracking consensus over dynamic random graphs: A linear system approach
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 12 July 2022, pp. 408-423
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Profiling ponded soil surface in saturated seepage into drain-line sink: Kalashnikov’s method of lateral leaching revisited
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 12 July 2022, pp. 367-384
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Enriques surfaces and an Apollonian packing in eight dimensions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 11 July 2022, pp. 205-221
-
- Article
- Export citation
On homomorphisms into Weyl modules corresponding to partitions with two parts
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 11 July 2022, pp. 272-283
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fluctuation response patterns of network dynamics – An introduction
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 11 July 2022, pp. 429-466
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

An Indefinite Excursion in Operator Theory
- Geometric and Spectral Treks in Kreĭn Spaces
-
- Published online:
- 08 July 2022
- Print publication:
- 28 July 2022
Homogeneous and curvature homogeneous Lorentzian critical metrics
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 1272-1296
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PEM series 2 volume 65 issue 2 Cover and Back matter
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 08 July 2022, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Graded comodule categories with enough projectives
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 257-271
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PEM series 2 volume 65 issue 2 Cover and Front matter
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 08 July 2022, pp. f1-f2
-
- Article
-
- You have access
- Export citation
7 - Compact Operators
-
- Book:
- Functional Analysis
- Published online:
- 23 June 2022
- Print publication:
- 07 July 2022, pp 229-258
-
- Chapter
- Export citation