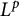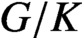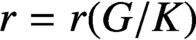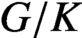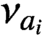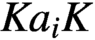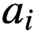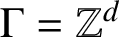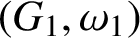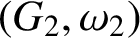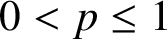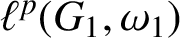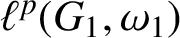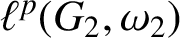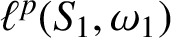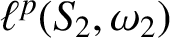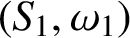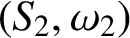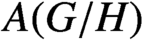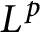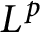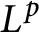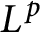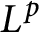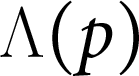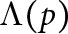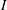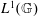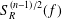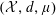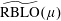Refine listing
Actions for selected content:
261 results in 43Axx
Oscillating multipliers on symmetric and locally symmetric spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 14 May 2021, pp. 887-905
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE SMOOTHNESS OF ORBITAL MEASURES ON NONCOMPACT SYMMETRIC SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 26 April 2021, pp. 188-207
- Print publication:
- October 2022
-
- Article
- Export citation
Convolution structures for an Orlicz space with respect to vector measures on a compact group
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 26 March 2021, pp. 87-98
-
- Article
- Export citation
A BIJECTION OF INVARIANT MEANS ON AN AMENABLE GROUP WITH THOSE ON A LATTICE SUBGROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 18 January 2021, pp. 302-307
- Print publication:
- October 2021
-
- Article
- Export citation
ON ALGEBRA ISOMORPHISMS BETWEEN p-BANACH BEURLING ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 11 January 2021, pp. 308-319
- Print publication:
- October 2021
-
- Article
- Export citation
SOME HOMOLOGICAL PROPERTIES OF FOURIER ALGEBRAS ON HOMOGENEOUS SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 132-140
- Print publication:
- August 2021
-
- Article
- Export citation
On isomorphisms between weighted
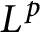 $L^p$-algebras
$L^p$-algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 853-866
- Print publication:
- December 2021
-
- Article
- Export citation
AMENABILITY AND ORLICZ FIGÀ-TALAMANCA HERZ ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 05 October 2020, pp. 218-229
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- Export citation
POINCARÉ AND SOBOLEV INEQUALITIES FOR DIFFERENTIAL FORMS IN HEISENBERG GROUPS AND CONTACT MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 29 June 2020, pp. 869-920
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
Ring-theoretic (In)finiteness in reduced products of Banach algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 29 June 2020, pp. 1423-1458
- Print publication:
- October 2021
-
- Article
- Export citation
INVARIANT MEANS AND ACTIONS OF SEMITOPOLOGICAL SEMIGROUPS ON COMPLETELY REGULAR SPACES AND APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 10 June 2020, pp. 162-173
- Print publication:
- February 2021
-
- Article
- Export citation
AN UNCERTAINTY PRINCIPLE FOR SOLUTIONS OF THE SCHRÖDINGER EQUATION ON
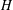 $H$-TYPE GROUPS
$H$-TYPE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 02 April 2020, pp. 1-16
- Print publication:
- August 2021
-
- Article
- Export citation
A Non-abelian, Non-Sidon, Completely Bounded
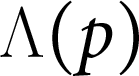 $\Lambda (p)$ Set
$\Lambda (p)$ Set
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 26 February 2020, pp. 1-7
- Print publication:
- March 2021
-
- Article
- Export citation
Translates of Functions on the Heisenberg Group and the HRT Conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 February 2020, pp. 871-881
- Print publication:
- December 2020
-
- Article
- Export citation
Ideals of the Quantum Group Algebra, Arens Regularity and Weakly Compact Multipliers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 January 2020, pp. 825-836
- Print publication:
- December 2020
-
- Article
- Export citation
BOCHNER–RIESZ MEANS ON BLOCK-SOBOLEV SPACES IN COMPACT LIE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 176-192
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
ZERO JORDAN PRODUCT DETERMINED BANACH ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 08 January 2020, pp. 145-158
- Print publication:
- October 2021
-
- Article
- Export citation
Amenability and Fixed Point Properties of Semitopological Semigroups in Modular Vector Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 16 December 2019, pp. 692-704
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
The John–Nirenberg Inequality for the Regularized BLO Space on Non-homogeneous Metric Measure Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 10 December 2019, pp. 643-654
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
ARENS PRODUCTS, ARENS REGULARITY AND RELATED PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 04 December 2019, pp. 138-150
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation