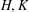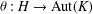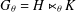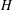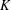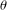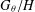Refine listing
Actions for selected content:
261 results in 43Axx
The automorphism group of a shift of slow growth is amenable
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 11 December 2018, pp. 1788-1804
- Print publication:
- July 2020
-
- Article
-
- You have access
- Export citation
A COMPACT QUALITATIVE UNCERTAINTY PRINCIPLE FOR SOME NONUNIMODULAR GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 114-120
- Print publication:
- February 2019
-
- Article
-
- You have access
- Open access
- Export citation
Amenability and unique ergodicity of automorphism groups of countable homogeneous directed graphs
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 17 October 2018, pp. 1351-1401
- Print publication:
- May 2020
-
- Article
- Export citation
HARDY’S THEOREM FOR GABOR TRANSFORM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 143-159
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
CONTINUOUS ASSOCIATION SCHEMES AND HYPERGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 July 2018, pp. 361-426
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Sobolev Algebras Through a ‘Carré Du Champ’ Identity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 24 July 2018, pp. 1041-1054
-
- Article
- Export citation
On Følner sets in topological groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1333-1361
- Print publication:
- July 2018
-
- Article
- Export citation
Hardy-Type Inequalities for Fractional Powers of the Dunkl–Hermite Operator
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 02 April 2018, pp. 513-544
-
- Article
- Export citation
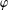 $\unicode[STIX]{x1D711}$ -CONTRACTIBILITY AND
$\unicode[STIX]{x1D711}$ -CONTRACTIBILITY AND 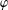 $\unicode[STIX]{x1D711}$ -CONNES AMENABILITY COINCIDE WITH SOME OLDER NOTIONS
$\unicode[STIX]{x1D711}$ -CONNES AMENABILITY COINCIDE WITH SOME OLDER NOTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 30 January 2018, pp. 274-278
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
The Point Value Maximization Problem for Positive Definite Functions Supported in a Given Subset of a Locally Compact Group
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 24 January 2018, pp. 179-200
-
- Article
- Export citation
APPLICATIONS OF AN INTERSECTION FORMULA TO DUAL CONES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 94-101
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Intertwined Markov processes: the extended Chapman–Kolmogorov equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 September 2017, pp. 123-131
- Print publication:
- February 2018
-
- Article
- Export citation
SOME CONVERGENCE THEOREMS IN FOURIER ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 03 July 2017, pp. 487-495
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
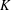 $K$ -SPHERICAL FUNCTIONS ON ABELIAN SEMIGROUPS
$K$ -SPHERICAL FUNCTIONS ON ABELIAN SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 13 June 2017, pp. 479-486
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
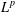 $L^{p}$ –
$L^{p}$ – 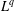 $L^{q}$ OFF-DIAGONAL ESTIMATES FOR THE ORNSTEIN–UHLENBECK SEMIGROUP: SOME POSITIVE AND NEGATIVE RESULTS
$L^{q}$ OFF-DIAGONAL ESTIMATES FOR THE ORNSTEIN–UHLENBECK SEMIGROUP: SOME POSITIVE AND NEGATIVE RESULTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 154-161
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
A remark on fullness of some group measure space von Neumann algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 02 November 2016, pp. 2493-2502
- Print publication:
- December 2016
-
- Article
- Export citation
COMPACT ELEMENTS AND OPERATORS OF QUANTUM GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 445-462
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
DUAL SPACE AND HYPERDIMENSION OF COMPACT HYPERGROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 421-435
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
Bruckner–Garg-Type Results with Respect to Haar Null Sets in C[0, 1]
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 10 May 2016, pp. 17-30
-
- Article
- Export citation
ABSTRACT HARMONIC ANALYSIS OF RELATIVE CONVOLUTIONS OVER CANONICAL HOMOGENEOUS SPACES OF SEMIDIRECT PRODUCT GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 171-187
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
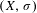
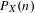
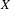
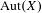
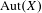
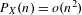
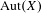
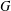
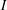
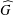
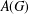
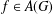
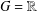
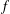
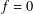
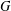
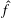
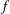
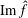
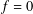
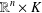
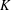
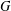
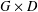
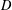
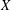
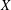
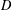
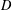
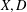
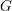
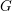
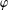
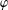
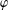
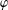
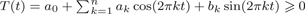
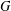
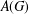
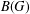
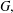

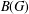
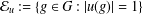
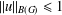
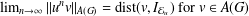
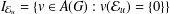
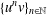
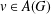
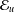
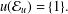
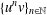
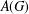
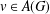
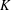








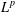
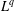
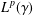
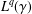
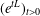

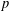
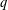

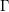
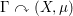
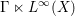
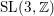
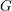
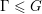
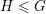
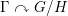
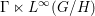
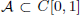 is
is 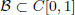 and a Borel probability measure
and a Borel probability measure 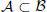 and
and 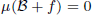 for all
for all