Refine listing
Actions for selected content:
261 results in 43Axx
POROSITY OF CERTAIN SUBSETS OF LEBESGUE SPACES ON LOCALLY COMPACT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 12 December 2012, pp. 113-122
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
Laguerre semigroup and Dunkl operators
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 18 May 2012, pp. 1265-1336
- Print publication:
- July 2012
-
- Article
-
- You have access
- Export citation
ON THE TOPOLOGICAL CENTRE OF L1(G/H)**
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 15 March 2012, pp. 119-125
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation
AN ARBITRARY INTERSECTION OF Lp-SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 16 February 2012, pp. 433-445
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
THE MODULUS OF WEAKLY COMPACT MULTIPLIERS ON THE BANACH ALGEBRA L1(𝒢)** OF A LOCALLY COMPACT GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 25 January 2012, pp. 315-321
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
Operator algebras from the discrete Heisenberg semigroup
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 08 November 2011, pp. 1-22
-
- Article
-
- You have access
- Export citation
ESSENTIAL CHARACTER AMENABILITY OF BANACH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 01 November 2011, pp. 372-386
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
STRICT TOPOLOGY AS A MIXED TOPOLOGY ON LEBESGUE SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 06 September 2011, pp. 504-515
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
AN EIGENSPACE OF LARGE DIMENSION FOR A HECKE ALGEBRA ON AN
 BUILDING
BUILDING
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 28 September 2011, pp. 29-54
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
ON HOMOLOGICAL PROPERTIES FOR SOME MODULES OF UNIFORMLY CONTINUOUS FUNCTIONS OVER CONVOLUTION ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 13 July 2011, pp. 177-185
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
Homological properties of certain Banach modules over group algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 07 April 2011, pp. 321-328
-
- Article
-
- You have access
- Export citation
CONVOLUTION OF ORBITAL MEASURES IN SYMMETRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 09 February 2011, pp. 470-485
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
THE SKITOVICH–DARMOIS THEOREM FOR LOCALLY COMPACT ABELIAN GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 11 June 2010, pp. 339-352
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Corrigendum: equivalent weights and standard homomorphisms for convolution algebras on ℝ+
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 415-417
-
- Article
-
- You have access
- Export citation
Amenability of ultrapowers of Banach algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 307-338
-
- Article
-
- You have access
- Export citation
Equivalent weights and standard homomorphisms for convolution algebras on ℝ+
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 409-418
-
- Article
-
- You have access
- Export citation
CONVOLUTIONS OF GENERIC ORBITAL MEASURES IN COMPACT SYMMETRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 05 May 2009, pp. 513-522
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
COMPACT LEFT MULTIPLIERS ON BANACH ALGEBRAS RELATED TO LOCALLY COMPACT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 227-238
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
ESSENTIAL AMENABILITY OF ABSTRACT SEGAL ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 319-325
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
A Plancherel formula for Sp2n/Spn×Spn and its application
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 501-527
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
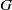
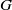
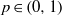
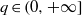
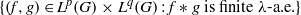
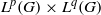
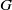
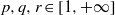
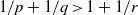
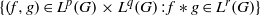
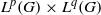
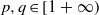
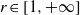
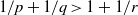
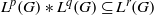
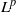
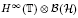 .
.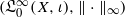 . Next, by showing that
. Next, by showing that 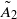 BUILDING
BUILDING
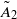 and let 𝔸 be its fundamental apartment. We consider the set 𝕌
and let 𝔸 be its fundamental apartment. We consider the set 𝕌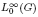 and
and 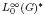 as Banach left
as Banach left 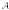 is Arens regular, and give some evidence that this is so if and only if
is Arens regular, and give some evidence that this is so if and only if 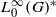 for a locally compact group
for a locally compact group 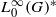 , and prove that the existence of a compact left multiplier on
, and prove that the existence of a compact left multiplier on 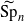 .
.