Refine listing
Actions for selected content:
261 results in 43Axx
The size of characters of exceptional lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 233-248
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
Ergodicity and stability of orbits of unbounded semigroup representations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 209-232
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
An uncertainty principle like Hardy's theorem for nilpotent Lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 1 / August 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 47-54
- Print publication:
- August 2004
-
- Article
-
- You have access
- Export citation
Higher Dimensional Cohomology of Weighted Sequence Algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 1 / August 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 57-68
- Print publication:
- August 2003
-
- Article
-
- You have access
- Export citation
A note on multipliers of Lp(G, A)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 25-34
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
Vector valued mean-periodic functions on groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 363-388
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
Discrete series of fusion algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 419-426
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
Hypergroups associated to harmonic NA groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 209-216
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
Calderón-type reproducing formulae on Lipschitz curves and surfaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 33-46
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
Pointwise estimates of the size of characters of compact Lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 61-84
- Print publication:
- August 2000
-
- Article
-
- You have access
- Export citation
The arithmetic of a semigroup of series of Walsh functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 3 / June 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 365-378
- Print publication:
- June 2000
-
- Article
-
- You have access
- Export citation
Pseudo differential operators on local Hardy spaces on chébli-teimèche hypergroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 2 / April 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 202-230
- Print publication:
- April 2000
-
- Article
-
- You have access
- Export citation
An Lp Version of the Hardy Theorem for Motion Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 1 / February 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 55-67
- Print publication:
- February 2000
-
- Article
-
- You have access
- Export citation
A family of strongly singular operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 1 / August 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 58-84
- Print publication:
- August 1999
-
- Article
-
- You have access
- Export citation
Lp-multipliers of mixed-norm type on locally compact Vilenkin groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 3 / December 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 370-387
- Print publication:
- December 1998
-
- Article
-
- You have access
- Export citation
Hilbert transform associated with finite maximal subdiagonal algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 3 / December 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 388-404
- Print publication:
- December 1998
-
- Article
-
- You have access
- Export citation
Amenability, lp-homologies and translation invariant functionals
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 1 / August 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 111-119
- Print publication:
- August 1998
-
- Article
-
- You have access
- Export citation
Ergodicity and differences of functions on semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 253-265
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
Lp–Lrestimates for the Poisson semigroup on homogeneous trees
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 20-32
- Print publication:
- February 1998
-
- Article
-
- You have access
- Export citation
Cesàro kernels on classical groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 3 / December 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 364-389
- Print publication:
- December 1997
-
- Article
-
- You have access
- Export citation
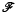 , the reduced Beurling spectrum of ø is empty if and only if ø ∈
, the reduced Beurling spectrum of ø is empty if and only if ø ∈ 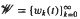 be the classical system of the Walsh functions,
be the classical system of the Walsh functions, 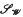 the multiplicative semigroup of the functions represented by series of functions
the multiplicative semigroup of the functions represented by series of functions 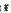 be a homogeneous tree of degree at least three. In this paper we investigate for which values of
be a homogeneous tree of degree at least three. In this paper we investigate for which values of 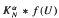 on the classical group
on the classical group 