Refine listing
Actions for selected content:
261 results in 43Axx
Regularity of spherical means and localization of spherical harmonic expansions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-297
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
Primitive ideals with bounded approximate units in L1-algebras of exponential lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 411-420
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
Translation invariant functionals on Lp (G) when G is not amenable
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 237-250
- Print publication:
- October 1986
-
- Article
-
- You have access
- Export citation
The ~ -representations of symmetric homogeneous algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 2 / April 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 267-275
- Print publication:
- April 1986
-
- Article
-
- You have access
- Export citation
Multipliers of Banach valued function spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 1 / August 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 51-62
- Print publication:
- August 1985
-
- Article
-
- You have access
- Export citation
Saturation on locally compact abelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 255-267
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
Bernstein and Jackson theorems for the Heisenberg group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 241-254
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
Denjoy-Bochner almost periodic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 205-222
- Print publication:
- October 1984
-
- Article
-
- You have access
- Export citation
Random Fourier series on compact abelian hypergroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 1 / August 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 45-81
- Print publication:
- August 1984
-
- Article
-
- You have access
- Export citation
A generalized Fourier transformation for L1(G)-Modules
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 3 / June 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 365-377
- Print publication:
- June 1984
-
- Article
-
- You have access
- Export citation
Constructions of the maximal strongly character invariant segal algebras and their applications
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 1 / August 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 123-131
- Print publication:
- August 1983
-
- Article
-
- You have access
- Export citation
Some non-critical idempotents in the closure of the characters in the maximal ideal space of M(D2)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 3 / June 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 293-305
- Print publication:
- June 1983
-
- Article
-
- You have access
- Export citation
Weyl functions and the Ap condition on compact lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 2 / October 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 185-192
- Print publication:
- October 1982
-
- Article
-
- You have access
- Export citation
Certain semigroups embeddabable in topological groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 1 / August 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 30-39
- Print publication:
- August 1982
-
- Article
-
- You have access
- Export citation
Remarks on multipliers on certain function spaces on groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 3 / October 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 276-288
- Print publication:
- October 1981
-
- Article
-
- You have access
- Export citation
Subordinate semigroups and order properties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 59-76
- Print publication:
- June 1981
-
- Article
-
- You have access
- Export citation
Harmonic analysis on the Fourier algebras A1, p(G)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 4 / April 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 438-452
- Print publication:
- April 1981
-
- Article
-
- You have access
- Export citation
Positive linear operators and the approximation of continuous functions on locally compact abelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 2 / December 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 180-186
- Print publication:
- December 1980
-
- Article
-
- You have access
- Export citation
Rudin synthesis on homogeneous Banach algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 29 / Issue 4 / June 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 407-416
- Print publication:
- June 1980
-
- Article
-
- You have access
- Export citation
Some multipliers on H1P(G)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 29 / Issue 1 / February 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 52-60
- Print publication:
- February 1980
-
- Article
-
- You have access
- Export citation
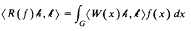
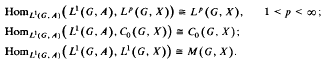
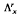 by the behavior of their best approximations by functions in the space
by the behavior of their best approximations by functions in the space 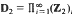 is contained in the closure of the characters D
is contained in the closure of the characters D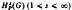 (
(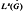 into
into 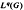 can be extended to a multiplier from
can be extended to a multiplier from 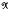 . For appropriate
. For appropriate 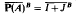 for some closed subalgebra
for some closed subalgebra 