Refine listing
Actions for selected content:
261 results in 43Axx
SKEW-PRODUCT DYNAMICAL SYSTEMS, ELLIS GROUPS AND TOPOLOGICAL CENTRE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 09 February 2009, pp. 129-145
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
ALGEBRAS ASSOCIATED WITH A FREE INVERSE MONOID
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 01 February 2009, pp. 27-31
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
WEIGHTED ESTIMATES FOR SINGULAR INTEGRAL OPERATORS WITH NONSMOOTH KERNELS AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 377-417
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
OPERATOR KERNELS FOR IRREDUCIBLE REPRESENTATIONS OF EXPONENTIAL LIE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 301-316
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
CONVOLUTION OPERATORS AND HOMOMORPHISMS OF LOCALLY COMPACT GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 329-344
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
I0 SETS FOR COMPACT, CONNECTED GROUPS: INTERPOLATION WITH MEASURES THAT ARE NONNEGATIVE OR OF SMALL SUPPORT
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 199-215
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
THE COMPLEX INVERSION FORMULA REVISITED
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 73-83
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
Generalized hypergroups and orthogonal polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 3 / June 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 369-394
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Generalized Gaussian estimates and riesz means of Schrödinger groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 2 / April 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-162
- Print publication:
- April 2007
-
- Article
-
- You have access
- Export citation
Fourier algebra of a hypergroup. I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 1 / February 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 59-83
- Print publication:
- February 2007
-
- Article
-
- You have access
- Export citation
Variations on a theorem of Cowling and Price with applications to nilpotent Lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 1 / February 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 11-27
- Print publication:
- February 2007
-
- Article
-
- You have access
- Export citation
The Gelfand transform of homogeneous distributions on Heisenberg type groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 3 / December 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-319
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation
Homomorphisms of the algebra of locally integrable functions on the half line
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 253-278
- Print publication:
- October 2006
-
- Article
-
- You have access
- Export citation
Some new Besov and Triebel-Lizorkin spaces associated with para-accretive functions on spaces of homogeneous type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 229-262
- Print publication:
- April 2006
-
- Article
-
- You have access
- Export citation
Local hardy and BMO spaces on non-homogeneous spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-182
- Print publication:
- October 2005
-
- Article
-
- You have access
- Export citation
Operator algebras related to Thompson's group F
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 231-241
- Print publication:
- October 2005
-
- Article
-
- You have access
- Export citation
Negative definite and Schoenberg functions on commutative hypergroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 1 / August 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 25-37
- Print publication:
- August 2005
-
- Article
-
- You have access
- Export citation
The spectral mapping property for p–multiplier operators on compact abelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 3 / June 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 423-428
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
Heat Kernels on homogeneous spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 109-147
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
An LP version of Hardy's theorem for the Dunkl transform
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 371-386
- Print publication:
- December 2004
-
- Article
-
- You have access
- Export citation
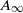 weights are established for singular integral operators with nonsmooth kernels via a new sharp maximal operator associated with a generalized approximation to the identity. As applications, the weighted
weights are established for singular integral operators with nonsmooth kernels via a new sharp maximal operator associated with a generalized approximation to the identity. As applications, the weighted  , let
, let 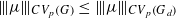 , for
, for 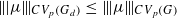 . These inequalities were already known for
. These inequalities were already known for 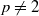 . Finally, for
. Finally, for 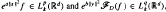 where
where 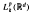 are the Lebesgue spaces associated with the Dunkl transform.
are the Lebesgue spaces associated with the Dunkl transform.