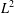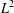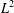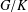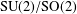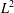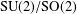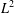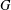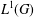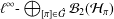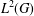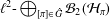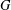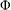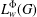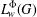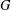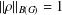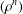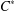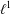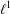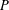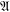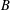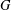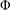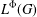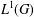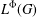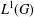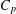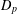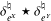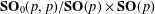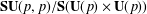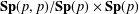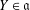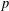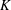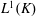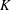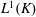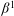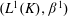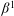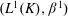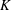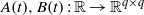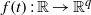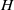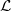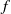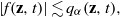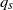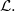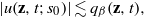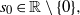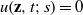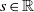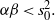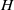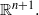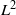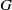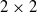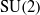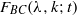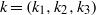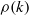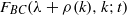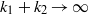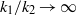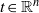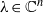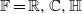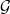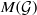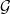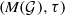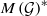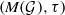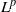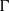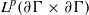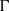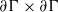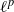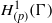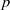Refine listing
Actions for selected content:
261 results in 43Axx
SMOOTHNESS OF CONVOLUTION PRODUCTS OF ORBITAL MEASURES ON RANK ONE COMPACT SYMMETRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 12 February 2016, pp. 131-143
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Orthogonally Additive Polynomials and Orthosymmetric Maps in Banach Algebras with Properties 𝔸 and 𝔹
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 15 December 2015, pp. 559-568
-
- Article
- Export citation
CHARACTERISATION OF THE FOURIER TRANSFORM ON COMPACT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 13 November 2015, pp. 467-472
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
FILTERED POLYNOMIAL APPROXIMATION ON THE SPHERE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 27 October 2015, pp. 162-163
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
WEIGHTED ORLICZ ALGEBRAS ON LOCALLY COMPACT GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 02 September 2015, pp. 399-414
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
ON ITERATED POWERS OF POSITIVE DEFINITE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 440-443
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
HOMOMORPHISMS OF
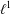 $\ell ^{1}$-MUNN ALGEBRAS AND APPLICATIONS TO SEMIGROUP ALGEBRAS
$\ell ^{1}$-MUNN ALGEBRAS AND APPLICATIONS TO SEMIGROUP ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 02 April 2015, pp. 115-122
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
A CONVOLUTION-INDUCED TOPOLOGY ON THE ORLICZ SPACE OF A LOCALLY COMPACT GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 19 January 2015, pp. 1-11
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
META-CENTRALIZERS OF NON-LOCALLY COMPACT GROUP ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 349-364
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
DIRECTLY FINITE ALGEBRAS OF PSEUDOFUNCTIONS ON LOCALLY COMPACT GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 693-707
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
CONVOLUTION OF ORBITAL MEASURES ON SYMMETRIC SPACES OF TYPE
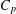 $C_{p}$ AND
$C_{p}$ AND 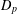 $D_{p}$
$D_{p}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 232-256
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
SOBOLEV SPACES ON LOCALLY COMPACT ABELIAN GROUPS AND THE BOSONIC STRING EQUATION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 39-53
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
HYPERGROUP ALGEBRAS AS TOPOLOGICAL ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 13 June 2014, pp. 486-493
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
ALMOST AUTOMORPHIC SOLUTIONS FOR DIFFERENTIAL EQUATIONS WITH PIECEWISE CONSTANT ARGUMENT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 26 November 2013, pp. 99-112
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
UNIQUENESS OF SOLUTIONS TO SCHRÖDINGER EQUATIONS ON
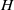 $H$-TYPE GROUPS
$H$-TYPE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 297-314
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
THE
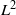 ${L}^{2} $-SINGULAR DICHOTOMY FOR EXCEPTIONAL LIE GROUPS AND ALGEBRAS
${L}^{2} $-SINGULAR DICHOTOMY FOR EXCEPTIONAL LIE GROUPS AND ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 24 July 2013, pp. 362-382
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
APPROXIMATE AMENABILITY OF SEGAL ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 18 July 2013, pp. 20-35
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
Limit transition between hypergeometric functions of type BC and type A
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 19 June 2013, pp. 1381-1400
- Print publication:
- August 2013
-
- Article
- Export citation
THE STRONG DUAL OF MEASURE ALGEBRAS WITH CERTAIN LOCALLY CONVEX TOPOLOGIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 08 April 2013, pp. 353-365
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Proper isometric actions of hyperbolic groups on
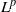 $L^p$-spaces
$L^p$-spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 5 / May 2013
- Published online by Cambridge University Press:
- 26 February 2013, pp. 773-792
- Print publication:
- May 2013
-
- Article
- Export citation