Refine listing
Actions for selected content:
261 results in 43Axx
Amenability and semisimplicity for second duals of quotients of the Fourier algebra A(G)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 3 / December 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 289-296
- Print publication:
- December 1997
-
- Article
-
- You have access
- Export citation
Algebraic characterizations of locally compact groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 405-420
- Print publication:
- June 1997
-
- Article
-
- You have access
- Export citation
Equivariant holomorphic maps into the Siegel disc and the metaplectic representation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 2 / April 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 160-174
- Print publication:
- April 1997
-
- Article
-
- You have access
- Export citation
S and g*λ-functions on compact Lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 3 / December 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 327-344
- Print publication:
- December 1996
-
- Article
-
- You have access
- Export citation
Exponentially bounded positive-definite functions on a commutative hypergroup
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 238-248
- Print publication:
- October 1996
-
- Article
-
- You have access
- Export citation
Derived intertwining norms for reducible spherical principal series
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-188
- Print publication:
- October 1996
-
- Article
-
- You have access
- Export citation
Asymptotic distributions for the Ehrenfest urn and related random walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 340-356
- Print publication:
- September 1996
-
- Article
- Export citation
The Plancherel formula for the horocycle space and generalizations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 1 / August 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 42-56
- Print publication:
- August 1996
-
- Article
-
- You have access
- Export citation
Weighted p-Sidon sets
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 1 / August 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 73-95
- Print publication:
- August 1996
-
- Article
-
- You have access
- Export citation
Characterization of lipschitz spaces on compact Lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 2 / April 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 200-209
- Print publication:
- April 1995
-
- Article
-
- You have access
- Export citation
Subelliptic operators on Lie groups: regularity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 179-229
- Print publication:
- October 1994
-
- Article
-
- You have access
- Export citation
Lp-functions satisfying the mean value property on homogeneous spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 3 / June 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 384-390
- Print publication:
- June 1994
-
- Article
-
- You have access
- Export citation
Harmonic analysis for groups acting on triangle buildings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 3 / June 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-383
- Print publication:
- June 1994
-
- Article
-
- You have access
- Export citation
Multipliers for Hardy spaces on locally compact Vilenkin groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 3 / December 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-301
- Print publication:
- December 1993
-
- Article
-
- You have access
- Export citation
BMO and singular integrals over local fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 3 / June 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 321-333
- Print publication:
- June 1993
-
- Article
-
- You have access
- Export citation
Rosenthal sets and the Radon-Nikodym property
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 2 / April 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 213-220
- Print publication:
- April 1993
-
- Article
-
- You have access
- Export citation
Multipliers from spaces of test functions to amalgams
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 1 / February 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 97-110
- Print publication:
- February 1993
-
- Article
-
- You have access
- Export citation
Fonctions propres de l'opérateur de Laplace-Beltrami associé au bi-disque
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-197
- Print publication:
- October 1992
-
- Article
-
- You have access
- Export citation
Amenability and ideals in A(G)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-155
- Print publication:
- October 1992
-
- Article
-
- You have access
- Export citation
Isomorphisms of hypergroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 3 / June 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 383-400
- Print publication:
- June 1992
-
- Article
-
- You have access
- Export citation
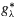 -functions.
-functions.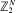 in continuous time
in continuous time 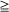 0 can be expressed in terms of binomial distributions; their limit behaviour for
0 can be expressed in terms of binomial distributions; their limit behaviour for 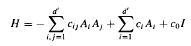
 of
of  be its set of vertices. We study a commutative algebra
be its set of vertices. We study a commutative algebra 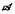 of ‘averaging’ operators acting on the space of complex valued functions on
of ‘averaging’ operators acting on the space of complex valued functions on 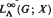 is separable then
is separable then