Refine listing
Actions for selected content:
108 results in 14Bxx
Slodowy slices and universal Poisson deformations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 09 November 2011, pp. 121-144
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
Fibers of generic projections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 02 February 2010, pp. 435-456
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Linear free divisors and Frobenius manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 23 October 2009, pp. 1305-1350
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Singularities on normal varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 393-414
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Deformation of finite morphisms and smoothing of ropes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 673-688
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
Higher Nash blowups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1493-1510
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
On the asymptotic behaviour of associated primes of generalized local cohomology modules
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 217-226
- Print publication:
- October 2007
-
- Article
-
- You have access
- Export citation
On the Gauss maps of singular projective varieties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 119-130
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
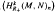 be the
be the 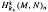 . In this paper we study the asymptotic behavior of Assf
. In this paper we study the asymptotic behavior of Assf 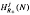 is not finitely generated.
is not finitely generated.