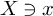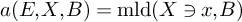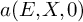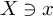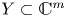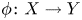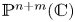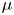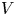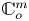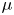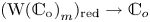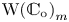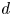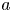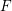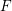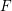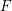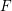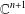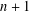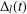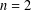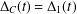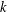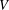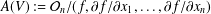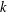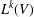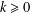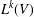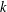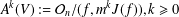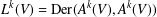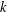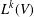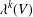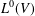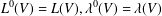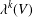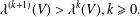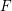Refine listing
Actions for selected content:
108 results in 14Bxx
Group actions on local moduli space of holomorphic vector bundles
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 August 2022, pp. 553-567
- Print publication:
- June 2023
-
- Article
- Export citation
Classification of singularities of cluster algebras of finite type: the case of trivial coefficients
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 04 July 2022, pp. 170-204
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON BOUNDEDNESS OF DIVISORS COMPUTING MINIMAL LOG DISCREPANCIES FOR SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 13 June 2022, pp. 2907-2930
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Fukui–Kurdyka–Paunescu conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 11 August 2022, pp. 1298-1313
- Print publication:
- June 2022
-
- Article
- Export citation
Newton non-degenerate
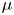 $\mu$-constant deformations admit simultaneous embedded resolutions
$\mu$-constant deformations admit simultaneous embedded resolutions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 11 August 2022, pp. 1268-1297
- Print publication:
- June 2022
-
- Article
- Export citation
On Lipschitz normally embedded complex surface germs
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 27 May 2022, pp. 623-653
- Print publication:
- March 2022
-
- Article
- Export citation
Embedding codimension of the space of arcs
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 February 2022, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A uniform treatment of Grothendieck's localization problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 57-88
- Print publication:
- January 2022
-
- Article
- Export citation
On minimal log discrepancies and kollár components
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 04 November 2021, pp. 982-1001
-
- Article
- Export citation
SIMPLICITY CRITERIA FOR RINGS OF DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 347-351
- Print publication:
- May 2022
-
- Article
- Export citation
Corrigendum: A curve selection lemma in spaces of arcs and the image of the Nash map
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 19 March 2021, pp. 641-648
- Print publication:
- March 2021
-
- Article
-
- You have access
- HTML
- Export citation
NOTES ON VANISHING CYCLES AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 29 October 2020, pp. 371-415
- Print publication:
- December 2020
-
- Article
- Export citation
ERRATUM: CONTINUITY OF HILBERT–KUNZ MULTIPLICITY AND F-SIGNATURE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 245 / March 2022
- Published online by Cambridge University Press:
- 23 October 2020, pp. 229-231
- Print publication:
- March 2022
-
- Article
- Export citation
THE LIPMAN–ZARISKI CONJECTURE IN GENUS ONE HIGHER
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 23 April 2020, e21
-
- Article
-
- You have access
- Open access
- Export citation
THE GAMMA CONSTRUCTION AND ASYMPTOTIC INVARIANTS OF LINE BUNDLES OVER ARBITRARY FIELDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 242 / June 2021
- Published online by Cambridge University Press:
- 23 September 2019, pp. 165-207
- Print publication:
- June 2021
-
- Article
- Export citation
Ascending chain condition for
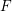 $F$-pure thresholds on a fixed strongly
$F$-pure thresholds on a fixed strongly 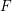 $F$-regular germ
$F$-regular germ
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 28 May 2019, pp. 1194-1223
- Print publication:
- June 2019
-
- Article
- Export citation
ON COMPLEX HOMOGENEOUS SINGULARITIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 27 May 2019, pp. 395-409
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Global Euler obstruction, global Brasselet numbers and critical points
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 14 May 2019, pp. 2503-2534
- Print publication:
- October 2020
-
- Article
- Export citation
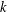 $k$TH YAU NUMBER OF ISOLATED HYPERSURFACE SINGULARITIES AND AN INEQUALITY CONJECTURE
$k$TH YAU NUMBER OF ISOLATED HYPERSURFACE SINGULARITIES AND AN INEQUALITY CONJECTURE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 30 April 2019, pp. 94-118
- Print publication:
- February 2021
-
- Article
- Export citation
Formality conjecture for K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 23 April 2019, pp. 902-911
- Print publication:
- May 2019
-
- Article
- Export citation