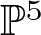Refine listing
Actions for selected content:
265 results in 14Cxx
Functional Transcendence of Periods and the Geometric André–Grothendieck Period Conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 23 June 2025, e97
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE REGULARITY INDEX OF FAT POINTS WHOSE SUPPORT IS CONTAINED IN A LINEAR PROPER SUBSPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 113 / Issue 1 / February 2026
- Published online by Cambridge University Press:
- 20 June 2025, pp. 90-97
- Print publication:
- February 2026
-
- Article
- Export citation
Abelian varieties with no power isogenous to a Jacobian
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 30 October 2025, pp. 1404-1457
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximal real varieties from moduli constructions
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limits of nodal surfaces and applications
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 April 2025, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kappa classes on KSBA spaces
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant divisors and equivariant line bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 April 2025, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A combinatorial formula for the nabla operator
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 800-830
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LINEAR SYSTEMS OF GEOMETRICALLY IRREDUCIBLE PLANE CUBICS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 27 February 2025, pp. 303-311
- Print publication:
- October 2025
-
- Article
- Export citation
“The six-functor formalism for rigid analytic motives” – Erratum
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 February 2025, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Positivity, plethysm and hyperbolicity of Siegel varieties in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 17 June 2025, pp. 257-304
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On families of K3 surfaces with real multiplication
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 January 2025, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A new generic vanishing theorem on homogeneous varieties and the positivity conjecture for triple intersections of Schubert cells
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 1-12
- Print publication:
- January 2025
-
- Article
- Export citation
On the Hilbert scheme of smooth curves of degree d = 15 in
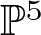 $\mathbb{P}^5$
$\mathbb{P}^5$
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 December 2024, pp. 1-38
-
- Article
- Export citation
A REMARK ON FUJINO’S WORK ON THE CANONICAL BUNDLE FORMULA VIA PERIOD MAPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 79-92
-
- Article
- Export citation
Vanishing theorem for tame harmonic bundles via L2-cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 03 April 2025, pp. 2828-2855
- Print publication:
- December 2024
-
- Article
- Export citation
Genus-zero r-spin theory
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The integral Chow ring of
 $\mathcal {M}_{1,n}$ for
$\mathcal {M}_{1,n}$ for  $n=3,\dots ,10$
$n=3,\dots ,10$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 November 2024, e103
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The line bundles on the moduli stack of principal bundles on families of curves
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 80-127
-
- Article
- Export citation
Non-torsion algebraic cycles on the Jacobians of Fermat quotients
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 60-72
- Print publication:
- March 2025
-
- Article
- Export citation